BSTより高速なデータ構造: Y-Fast Trie [UEC Advent Calendar 2024] 12日目
Published on 2024-12-12Last Modified 2025-01-02
Table Of Contents
まえがき
こんにちは、 InTheBloom です。 今年もUECアドカレの季節がやってきましたね。Twitterでカレンダーが生えたのを観測したので、これ幸いと枠をいただきました。これで3年目になります。
このエントリはUEC Advent Calendar 2024の12日目を担当します。 遅刻しました。すみません!
また、今年もUEC2が建っています。こちらもぜひどうぞ。
11日目はえぐちさんの Proxmoxの運用Tips【自宅鯖】 でした。 自宅鯖という単語、非常に魅力的に感じます。とは言いつつ、前提知識がなさすぎて大半が呪文に見えました。勉強が必要そうです。
UEC2ははんかくさんが担当ですが、まだアップされていないみたいです。
今年も力作ぞろいです。これからのエントリも楽しみですね!
はじめに
このエントリでは、Y-Fast Trie(ワイ-ファスト トライ)と呼ばれるデータ構造の動作原理を説明し、実際に組んだものを示します。 Y-Fast Trieの美しさ、ロマンを体感してください!
誤りの指摘は随時募集しています。指摘いただいたものは随時修正していきますので、お気軽にどうぞ。
一部、厳密性にかける部分があるかもしれません。 このエントリの情報は裏を取ってから使用することをお勧めします。
Y-Fast Trieの概要
Y-Fast Trieは非負整数値に対して各種操作を提供するデータ構造です。
データ構造とは何かについて厳密に定義を与えるのは難しいです。 ここでは、大まかに、できる操作の集合と、操作を実現する具体的なアルゴリズムをひとまとめにしたものをデータ構造と呼ぶことにしましょう。
前者をインターフェース、後者を内部実装と呼ぶことにします。
性能を議論する上で、各種操作をどれくらい効率よく、どれくらい省メモリで行えるかが知りたいです。 そこで、本文書内ではインターフェースを考えるとき、同時に各種操作の時間計算量と、データ構造全体が必要とする空間計算量に言及します。
計算量というのは、かかる時間や必要な領域を定量的に評価するための概念です。 詳細は 計算量について(外部リンク) を参照してください。
例えば、C++のstd::vectorは
- $i$番目の要素への読み書き: $O(1)$時間
- 要素を末尾へ挿入: 平均して$O(1)$時間
というインターフェースを提供するデータ構造です。空間計算量は、確保した列の長さ$N$に対して、$O(N)$です。 空間計算量が$O(N)$であるとは、格納した値や補助のデータを含めて$O(N)$byteしか必要としないことを表します。
Y-Fast Trieのインターフェース
Y-Fast Trieは、扱う整数の範囲を$\lbrack 0, 2 ^ w - 1 \rbrack$としたとき、以下のインターフェースを提供します。
| 操作 | 内容 | 時間計算量 |
|---|---|---|
| $\mathrm{insert}(x)$ | 集合に$x$を追加する | $\text{expected } O(\log(w))$ |
| $\mathrm{remove}(x)$ | 集合から$x$を削除する | $\text{expected } O(\log(w))$ |
| $\mathrm{successor}(x)$ | 集合に含まれる$x$以上最小の値を返す | $\text{expected } O(\log(w))$ |
| $\mathrm{predecessor}(x)$ | 集合に含まれる$x$以下最大の値を返す | $\text{expected } O(\log(w))$ |
$\text{expected}$という表記はその操作にかかる時間が確率変数で表現されることを表します。値はその期待値です。
このインターフェースは predecessor problem と呼ばれる有名な問題そのものです。 通常、内部実装として 赤黒木 や AVL木 といった二分探索木が使用されます。二分探索木を使用する場合、各操作は全体の操作回数を$N$として、$O(\log(N))$時間になります。 一方、Y-Fast Trieは$N$に依存することなく、常に$O(\log(w))$時間を保ちます。
$w$は整数を表現するのに必要なビット数であり、ほとんどのケースで$w \leq 64$になります。自然な仮定の元ではY-Fast Trieは二分探索木よりも理論的に高速です。
驚くべきことに、Y-Fast Trie空間計算量は$O(N)$です。 扱う値を非負整数に絞ることにより、二分探索木と同等レベルに省メモリかつ、確率的な平均計算量として見たときに、二分探索木より高速な操作を提供します。
前置きはここまでです。次の章からはY-Fast Trieの動作原理を見ていきましょう。
Binary Trieとsuccessorの探索
グラフ
Y-Fast Trieの仕組みを理解するためには、trie木を知る必要があります。 trieはグラフの一種です。グラフとは、頂点集合$V$と頂点間を結ぶ辺集合$E$の組のことで、ものともののつながりかただけを抜き出した数学モデルです。
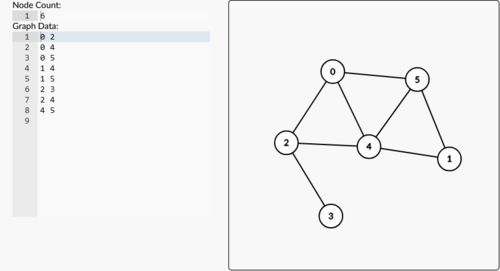
これがグラフです。この場合、頂点数が6で、辺数が8です。 Graph Editor でビジュアライザを試すことができます。
プログラム上でグラフを表現するときは通常、隣接リストを用いた表現を使います。 これは、各頂点に対応する構造体をつくり、辺を別の構造体へのポインタで表すものです。 以下に疑似コードを示します。
struct vertex { // vertex: 「頂点」の意
Data data; // 頂点番号や、それ以外の値をもたせることもある
vertex *[] adj; // 自分から辺がある頂点へのポインタ
// その他、辺に重みをつけることもある
}
うまく実装すると、$O(\vert V \vert + \vert E \vert)$の空間でグラフを表現することができます。
trie木
trieは、文字列の集合を表現する木です。
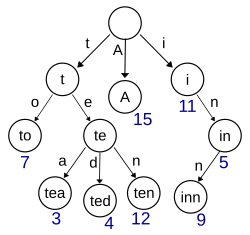
これがtrie木です。この木の場合、“A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn"から構築されています。 wikipediaの トライ からパブリックドメインの画像をお借りしました。( source )
trie木は常に次のルールに従っています。
- 根と呼ばれる「スタート地点」をもつ。
- 各辺には文字が割り当てられる。
- 根は空文字列を表現する。他の頂点は、根からそこまでたどったときに通った辺の文字を連結した文字列を表現する。
trieに文字列を追加するときは、根から出来るだけ既存の頂点を経由して文字を伸ばしていけばよいです。(図A)
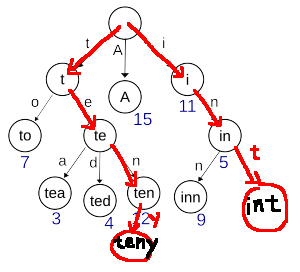
図A: “int"と"teny"の追加
削除するときは、その文字列を表現する頂点からはじめて、他の文字列に影響しない部分の頂点を削除しながら根までのぼっていけばよいです。(図B)
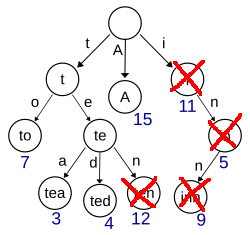
図B: “inn"と"ten"の削除
これらの操作は文字列$S$に対して$O(\vert S \vert)$時間で行うことができます。したがって、trieは文字列の集合に対して次の操作が可能です。
- $\mathrm{insert}(S)$: 文字列$S$を集合に追加する。$O(\vert S \vert)$時間
- $\mathrm{remove}(S)$: 文字列$S$を集合から削除する。$O(\vert S \vert)$時間
- $\mathrm{find}(S)$: 文字列$S$が集合に含まれるか確認する。$O(\vert S \vert)$時間
また、数を任意の進数で表現すると、文字列としてみなせるため、数に対しても$\mathrm{insert}, \mathrm{remove}, \mathrm{find}$を行うことができます。
jumpポインタと葉ノードの連結によるsuccessorへの対応
この先はtrieで数を扱うことを前提とします。留意してください。
簡単のため、trieで扱う数の基数を2に固定します。 これによりtrieの各ノードは高々2本の辺を持つことになります。これを特にbinary trieと呼びます。
また、扱う数を高々$w$文字で表現できると仮定し、最上位bitが1文字目に来るようにします。$w$文字に満たない場合はleading zeroをつけて対応します。 つまり、$w = 5$のとき、0は00000、3は00011、5は00101という文字列として扱います。
今導入した最上位bitから順に並べるルールにより、次の性質が保たれます。
- すべての葉は同じ高さにある。
- 任意のノードについて、$(\text{左に進んでからたどり着く任意の葉の値}) < (\text{右に進んでからたどり着く任意の葉})$が成立
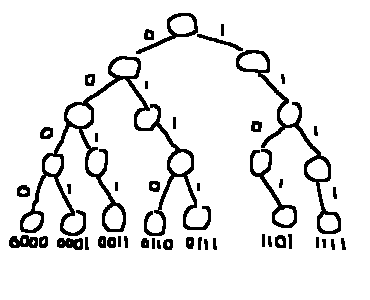
binary trieの例
だんだん二分探索木っぽくなってきました。
葉を左から見たときに値の昇順になるため、$\mathrm{successor}(x)$や$\mathrm{predecessor}(x)$は$x$を表す葉のすぐそばに存在します。 ここにさらにもう一工夫を行うと、ようやく$\mathrm{successor}, \mathrm{predecessor}$に対応できるようになります。
- 葉ノード間に辺をはり、連結リストのようにする。
- 子をひとつしか持たない中間ノードから、successorやpredecessorのすぐ近くになるはずの葉にジャンプ辺をはる。
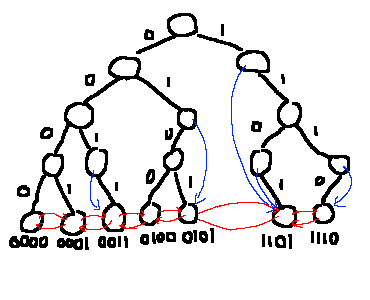
左右辺とジャンプ辺をはったbinary trie
一つ目についてはわかりやすいと思います。つまり、葉ノードだけ特別に「左右方向」の辺を持たせて、ひとつ大きい要素とひとつ小さい要素に飛べるようにするということです。
二つ目は、それそのものとしてはそこまで役に立ちません。葉の連結リスト化を動的に行うための補助データという役割が大きいです。「すぐ近くになるはずの葉にジャンプ辺をはる」というのは、具体的には、次の二つのどちらかを行います。
- 左の子を持たない場合: 右部分木最小の葉へジャンプできるようにする
- 右の子を持たない場合: 左部分木最大の葉へジャンプできるようにする
これで$\mathrm{successor}(x)$と$\mathrm{predecessor}(x)$に答える準備ができました。 このジャンプ辺と連結リストを利用して、次のように解答します。(両者ほぼ同じなので、successorのみ説明します。)
- $x$を2進表示した文字列を用いて、すでにある頂点をできるだけたどる。
- 葉にたどり着くことができれば、$x$を返却して終了。
- 左方向に進めない場合、$\mathrm{successor}(x)$はその頂点のジャンプ辺でたどり着く頂点である。右方向の場合、ジャンプ辺でたどり着く頂点よりひとつ大きい頂点である。
例として、上図のtrieにおいて$\mathrm{successor}(6)$を呼び出すとどうなるか見てみましょう。
6は0110なので、根から左、右と進みます。次に右に進むべきですが、辺がありません。そこで、ジャンプ辺を利用して左部分木最大の0101(5)にジャンプします。ここから連結リストで一つ右に移動し、1101(13)を手に入れることができます。図より、正しい解が返ってきていることがわかると思います。
計算量はやはり検索文字列の長さに依存し、$O(w)$時間です。
残る問題はどうやって要素の追加/削除時に連結リスト及びジャンプ辺を正しく保つかとなります。
追加
まず、通常のtrieと同様に頂点を追加します。今までなかった値を追加するわけなので、辺のない方向に進む瞬間が必ずあります。 そのタイミングでジャンプ辺を利用し、追加する頂点のsuccessorまたはpredecessorを取得します。これを用いて連結リストを繋ぎかえます。
ジャンプ辺の更新も行います。ジャンプ辺は自身の部分木の頂点に飛ぶことになっていました。 逆に言うと、新しく追加した頂点から根まで登っていく際に通る頂点を更新できれば十分です。
新しく頂点を追加したことで子が2になった頂点はジャンプ辺を外します。 そうでない場合、ジャンプ辺が未登録であるか、または新しい頂点のほうが今よりジャンプ先として適切かを判定すればよいです。
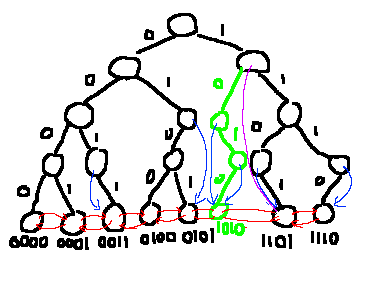
1010の追加。紫のジャンプ辺を利用して連結リストに組み込む。(このジャンプ辺は追加後削除される。)
削除
まず、葉を連結リストから外します。 あとは通常のtrie同様に、葉からはじめて、もともと子が2だった頂点に出会うまで頂点を消していきます。(葉だけはまだ使うので、まだメモリ解放はしません。)
最後にジャンプ辺の更新を行います。これも追加のときと同様に、根までさかのぼる道中にいる頂点のみ更新すればよいです。 そのような頂点であって、もともと自分をジャンプ先に登録していた頂点に出会ったとき、新しくジャンプ先になりうるのは葉のひとつ前かひとつ後ろになります。 したがって、消さずにとっておいた葉の連結リストを用いて適切に更新すればよいです。
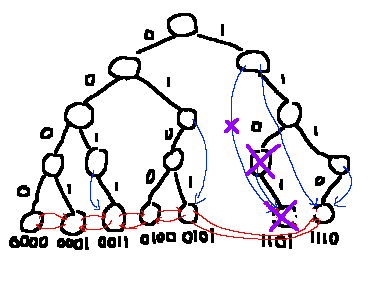
1101の削除。1のジャンプ辺が1101から1110へ更新される。
少々雑な紹介になってしまいましたが、基本的には登って下って以上の操作を必要としません。これらも$O(w)$時間で行うことができます。
まとめ
数を固定長さで最上位桁からみる文字列として扱い、葉ノード間の連結リスト、ジャンプ辺の概念を導入することで、binary trieは$\mathrm{insert}, \mathrm{remove}, \mathrm{successor}, \mathrm{predecessor}$を$O(w)$時間で行うことができる。
使用する領域は、ひとつの数あたり$O(w)$個の頂点が必要なため、$O(Nw)$となる。($N$が大きくなるほど新しく追加する頂点が減る傾向があることに注意。$N \ll 2 ^ w$であるときは$O(Nw)$より厳しく評価するのが難しいはず。)
X-Fast Trie
前章では、binary trieを用いた$\mathrm{insert}, \mathrm{remove}, \mathrm{successor}, \mathrm{predecessor}$への対応方法を説明しました。 基本的なアイデアはそのままに、少し拡張を加えることで、$\mathrm{successor}, \mathrm{predecessor}$の計算量を$\text{expected } O(\log(w))$時間に改善したデータ構造がX-Fast Trieです。
アイデア
binary trieでは、検索を行う中ではじめて進めなくなる頂点を見つけ、その頂点のジャンプ辺を用いてクエリにうまく解答していました。 この「はじめて進めなくなる頂点」を高速に見つけられるようにします。
具体的には、各階層にハッシュマップを持って、今その階層にある頂点をすべて登録し、深さに対して二分探索を行います。
ハッシュマップとは、大雑把に言えば
- 要素の追加と削除
- ある要素が今含まれているかどうか
を$\text{expected } O(1)$時間で判定するデータ構造です。より詳しいことはほかの情報源を参照してください。
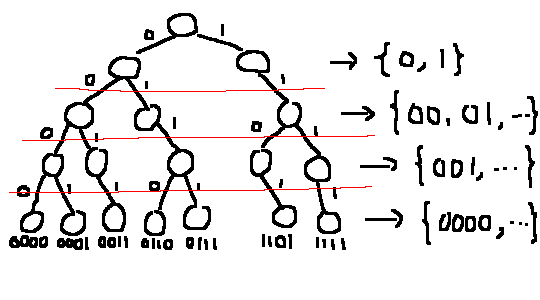
X-Fast Trie。各階層の頂点を登録している。
二分探索について少し補足します。 ある検索キー$x$を与えられたとき、$x$の上位$k$bitがtrieに含まれているか?という問題を考えます。これは$k$について単調です。 すなわち、$k = 0$は必ず真ですが、ある$k = a$で偽になったとすると、以降真になることはありえません。この境界点を二分探索で探します。
境界点さえ見つかってしまえば、あとは$O(1)$回の移動で目的の葉を見つけることができます。 したがって、計算量は木の高さ$w$を$\log$にしたものになります。binary trieからさらに減って$\text{expected } O(\log(w))$時間です。(ハッシュマップの$\text{expected}$がこちらに影響してしまいます。)
例として、上図において1100を探すことにします。
- まず、根を高さ0として、高さ2のハッシュマップを見ます。
- 高さ2のハッシュマップに11が含まれているので、より下の高さのみを考えればよいことがわかります。
- 次に高さ3に110が含まれているかを見ます。ここにもまだ含まれています。
- 最後に高さ4に1100が含まれているかを見ます。ここではもう含まれていません。
- この時点で高さ3に含まれ、高さ4に含まれないことがわかっています。差が1なので、境界が見つかったことになります。
よって、最後に含まれていた高さ3のハッシュマップに、キー110で登録されている頂点からジャンプ辺で飛ぶとよいです。
各種操作
追加削除はbinary trieとほとんど同じです。ひとつ異なるのが、
- 追加操作で新しい頂点を作る
- 削除操作で頂点を削除する
これらのタイミングでハッシュマップにも登録、削除を行う必要があります。 検索は上述したとおりです。
まとめ
X-Fast Trieはbinary trieの各層にハッシュマップを導入したデータ構造である。
この工夫により、$\mathrm{insert}, \mathrm{remove}$を$O(w)$時間、$\mathrm{successor}, \mathrm{predecessor}$を$\text{expected } O(\log(w))$時間で行うことができる。
使用する領域は変わらず$O(Nw)$となる。(ハッシュマップはうまく実装されていれば$N$個のキー挿入時に$O(N)$領域しか必要ないため、binary trieと比較して定数倍しか膨らまない。)
(補足: ハッシュマップは償却計算量が入ることがあると思いますが、このあたりを$\text{expected}$などと合わせたときにどう扱うのかについて、文献を探しても見つかりませんでした。なので、基本的には期待計算量に含まれるという体で書いています。)
Y-Fast Trie
とうとうメインディッシュがやってきました。
X-Fast Trieは検索こそ早いものの、追加と削除が低速でした。また、使用する領域も二分探索木に比べて$w$倍大きいです。 この二つの問題は密接にかかわっています。trieへの要素の追加削除にかかる時間や使用する領域の大きさは、真面目にすべてのノードをtrieで扱うとすると高さが減らない限り減りません。
そこで、Y-Fast Trieでは、trie部分で扱うノードを効率的に間引き、残りの要素の管理を別のデータ構造に委託する戦略をとります。
アイデア
Y-Fast Trieの性能が二分探索木の性能より良い理由は、$w \ll N$であるからでした。 逆に言うと、$N$が十分小さいことが保証できる状況であれば、二分探索木を利用することができます。 また、二分探索木はtrie系のデータ構造と異なり、一つの要素のために$O(w)$領域を必要としません。
そこで、本来trie側で扱う頂点集合をいくつかのグループに分けて、ひとつのグループをひとつの二分探索木に管理させることにします。 こうすることで、二分探索木のメリットを全て享受することを狙います。
つまり、どうにかして下図の状況が常に成立するようにします。(三角形は二分探索木、上はX-Fast Trieです。)
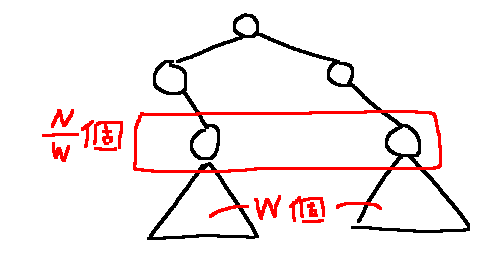
Y-Fast Trie。二次構造として、二分探索木を利用する。
X-Fast Trieに登録されている$O(N / w)$個のデータを昇順に$x _ 0, x _ 1, \dots$とし、$x _ i$の場所にある二分探索木は、区間$\lbrack x _ {i - 1}, x _ i \rbrack$に含まれる数を管理するとします。
もし、挿入されるデータがあらかじめわかっていれば、$x _ i$としてどれを選べばよいかがわかります。 しかし、今回の問題ではどんな値が来るか先に知ることができません。
そこで、ランダム性を用いて解決します。 新しくキーを挿入するとき、確率$1 / w$でX-Fast Trieに新しい二分探索木を登録し、そうでないときにはおとなしく既存の二分探索木で管理することにします。 たったこれだけで、ある時点での二分探索木が管理するデータの数の期待値を$O(w)$個にすることができます。
二分探索木のサイズ解析の概要
簡単に概要を説明します。 ある時点において、Y-Fast Trie全体が管理するデータを昇順に$y _ 0, y _ 1, \dots$とします。
ここで、$y _ i$を含む二分探索木の大きさは、$i$以前/以降ではじめて$1 / w$を引いた場所の二つで確定します。$i$より前を$p$、後を$q$とします。 これは、$i$からスタートして、確率$1 / w$でストップ、確率$1 - 1 / w$で次に進むという試行を右方向と左方向に行っていると考えることができます。
このようにして、$y _ i$を含む二分探索木が大きさ$k$をとるときの確率$p _ k$が算出することができます。各事象における確率がわかったので、大きさの期待値も計算できます。 そしてその期待値は$O(w)$になっています。
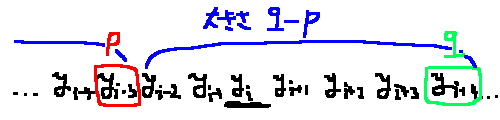
二分探索木のサイズがiから左右に伸ばした2点で確定することの視覚的イメージ
性能の解析
$\mathrm{insert}$について考えます。確率$1 / w$でX-Fast Trieへの追加を行い、$O(w)$時間がかかります。
確率$1 - 1 / w$で対応する二分探索木に追加を行います。対応する二分探索木を探すのはX-Fast Trieの検索によって行うので、$O(\log(w))$時間、二分探索木は大きさ$O(w)$程度であることが期待されるので、こちらも$O(\log(w))$時間です。
よって、これらの期待値は$O(\log(w))$時間になります。
$\mathrm{remove}$を考えます。キーが含まれる二分探索木の検索、その二分探索木からの削除はともに$O(\log(w))$時間です。
確率$1 / w$でX-Fast Trie側に登録しているキーを削除するケースを引きます。この場合、ひとつ右の二分探索木へ、自分の二分探索木をマージします。
ひとつ右の取得はX-Fast Trieの葉にある隣接リストを用いて$O(1)$時間で行うことができます。 二分探索木は$O(w)$個程度の要素を含むことが期待されるので、二分探索木のマージは$O(\log(w))$時間、X-Fast Trie側のノードの削除は$O(w)$時間になります。
よって、こちらも期待値は$O(\log(w))$時間です。
検索についてはすでに説明した通りです。
まとめ
Y-Fast TrieはX-Fast Trieに$O(N / w)$個の二分探索木を持たせたデータ構造である。この二分探索木を追加するとき、それぞれが管理する要素の期待値が$O(w)$となるように工夫を行う。これらにより、$\mathrm{insert}, \mathrm{remove}, \mathrm{successor}, \mathrm{predecessor}$を$\text{expected } O(\log(w))$時間で行うことができる。
実装例 + 実測
ここまで、動作原理の説明に終始してきました。 しかし、実際に動作するように組み上げるのは原理を理解する以上に大変です。 今回、机上の空論で終わらせないために、実装にチャレンジしました。(想定通りものすごく苦戦して、アドベントカレンダーに遅刻してしまいましたorz)
https://github.com/InTheBloom/YFastTrie
今回説明しきれなかったハッシュマップの実装や、二分探索木の実装もすべて含んでいます。 ある程度新しいD言語処理系をインストールした環境であれば実際に動かすことができます。 興味のある方は是非ご覧ください。
また、このような複雑なデータ構造は定数倍が悪いという話があります。そのあたりも検証するため、 Library Checker の問題で検証を行いました。 以下に、いくつかの提出リンクを示します。 (注意として、今回の実装は細かい最適化などをほとんど行っていません。かなり遅い実装なはずです。)
- Treap (6485ms)
- Binary Trie (メモリ超過によるRE | 4280ms)
- X-Fast Trie (メモリ超過によるRE | 6293ms)
- Y-Fast Trie (細かいチューニングによりギリギリMLEを回避 | 5896ms)
結論としては、存外Y-Fast Trieも悪くない感じでした。Binary TrieやX-Fast Trieに比べて明らかに空間使用量が減っていますし、Treapより速いのは驚きました。
参考資料 (あなたもY-Fast Trie組みませんか?)
-
みんなのデータ構造、Pat Morin著、堀江慧、陣内佑、田中康隆訳、ラムダノート
- 5章、6章、7章、13章が特に関係します。本エントリの主情報源です。
- なんと、 ここで 無料で読めます。知らなかったので2000円払って買いました。(存外紙ベースのほうも悪くないです。)
-
プログラミングコンテストでのデータ構造2 ~平衡二分探索木編~、秋葉拓哉著、 https://www.slideshare.net/slideshow/2-12188757/12188757
- さっくりと解説されているので、初めての人はこれだけ見て組むのはしんどいです。(1敗) 他のリソースも活用することをお勧めします。
-
Predecessorを高速に解くデータ構造: Y-Fast Trie、goonew著、 https://qiita.com/goonew/items/6ffac4b5e48dc05ca884
- たくさんの図があり、丁寧に解説されています。binary trieでsuccessorクエリをサポートする方法が特にわかりやすいです。
-
Predecessor Problem、 https://judge.yosupo.jp/problem/predecessor_problem
- 自力で行うより信頼性が高いテストを行うことができます。
-
Associative Array、 https://judge.yosupo.jp/problem/associative_array
- 上に同様です。
終わりに
アドベントカレンダーに寄せるエントリということで、かなり気合が入ってしまい、超長文を生成してしまいました。 ここまで見ていただいた方、本当にありがとうございました。
Y-Fast Trieの動作原理を自分なりにできる限りかみ砕いて説明したつもりです。皆さんはどう感じましたか? 私のささやかな願いとして、このエントリをみて、調布駅のTrieを「トライ」と読んでしまう人が増えるといいなと思っています。
感想、質問などを寄せていただけると非常に喜びます。私の twitter までどうぞ。
さて、アドベントカレンダーは続きます。 12月13日はAmiciiさんの担当です。 また、UEC2はazarasingさんによる Youtube プレイヤーのサイドに出てくる動画群が気に入らないので常に「関連動画」が出てくるようにする拡張機能を雑に作った。 です。
次のエントリも是非ご覧ください!