ミスりにくい二分探索 [UEC Advent Calendar 2023] 6日目
Published on 2023-12-05Last Modified 2023-12-06
Table Of Contents
まえがき
この記事は、 電通大生による電通大生のためのUEC Advent Calendar 2023 の6日目担当です。
2時間ほど遅刻しました!すみません!
5日目はトナカイさんによる、 BASHであそぼ でした。 私もⅠ類の友人がいますが、彼は毎回提出コマンドを手打ちしていた記憶があります。 自動化スクリプトをbashでササッと組めるのすごく憧れるんですが、いつもbashを勉強する面倒臭さが勝ってしまいます。 私もいつの日か 退屈なことはpythonにやらせ られるようになりたいです。
実はAdvent Calendarは公開後すぐに枠が埋まってしまったので、2枠目も存在します(なんで?)。
5日目の牛田ウシタさんの記事はまだ公開されていないようですが、こちらもぜひ読んでみてはいかがでしょうか!
本記事を書いている間に更新されていました。 アドカレを書くためにいきなり22万吹き飛んでいて笑いました。 長期間の出来事が詳細に語られていて、臨場感がありました。私が文章書くと臨場感が死ぬので、すごいなぁ。。
私は関西に住んでいた経験があるため、いくつか知っているポイントがあったのが面白かったです。(京都のデカい階段、奈良の穴とか)
それではそろそろ本題に行きましょう。
はじめに
こんにちは、こんばんは、おはようございます。 6日目を担当する、 In と申します。 去年に引き続き、今年も参加させていただきました。
今年は 去年のやつ よりも実りのある記事がかければ良いなと思っております。よろしくおねがいします。
二分探索とは
本記事では、競技プログラミングでよく使うかつ、割とバグらせやすいと思っているアルゴリズムである二分探索の 比較的バグらせにくい実装を紹介します。
なお、厳密性を欠いていたり、不正確な情報があるかもしれません。 もしまずい場所があれば指摘していただけると助かります。
まずは、本記事において「二分探索」が何を指すのかをはっきりさせておきましょう。
関数$f: \mathbb{Z} \rarr \{0, 1 \}$であって、次の性質を満たすものを考える。
- $f(x)=0$を満たす$x \in \mathbb{Z}$が少なくとも一つ以上存在する。
- $f(y)=1$を満たす$y \in \mathbb{Z}$が少なくとも一つ以上存在する。
- 次のどちらか片方のみが成立している。
- $x \leq y \Rightarrow f(x) \leq f(y)$
- $x \geq y \Rightarrow f(x) \leq f(y)$
$f(a)=0$、$f(b)=1$を既知として、任意の$\mathbb{Z}$の元に対して$f$の値を時間計算量$\alpha$で求められるとする。 この時、$f(x) \neq f(x+1)$なる$x$を時間計算量$O(\alpha \log{|a-b|})$で求める。
状況はこんな感じです。
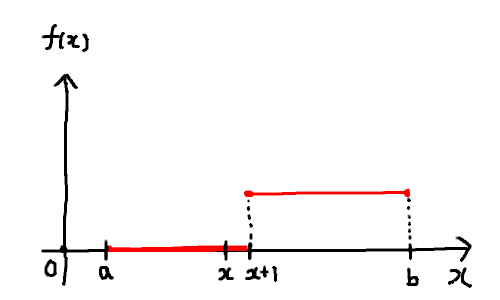
二分探索の動作原理はいたってシンプルです。 最初、$a$と$b$の中点$c$をとります。 具体的には、$c = \lfloor \frac{a+b}{2} \rfloor$とします。
仮定より、関数$f$の値はある一点で$0$と$1$が切り替わり、それ以外の場所で変化しません。 ゆえに、もし$f(c)=0$であったとすると、必ず$a \leq c \leq x$であることがいえ、そうでない時は$x+1 \leq c \leq b$が言えます。
$f(c)$の値によって区間の端点$a$か$b$を$c$で置き換えます。これを繰り返します。
結果的に、$f(a)=0$と$f(b)=1$を保ったまま、$|b-a|=1$となるまで区間を縮めることができます。
時間計算量を考えましょう。 区間の端点を一度置き換えるごとに区間の長さはおよそ$\frac{1}{2}$になります。 したがって、アルゴリズムが停止するまでに繰り返される回数は、 $$ \begin{equation*} \begin{split} \frac{|b-a|}{2^x} &= 1 \\ |b-a| &= 2^x \\ \end{split} \end{equation*} $$ より、$x = \log_2{|b-a|}$となり、$O(\log{|b-a|})$回程度である事がわかります。
実装の詳細
競技プログラミング界隈で「めぐる式二分探索」と呼ばれる実装があります。
【めぐるのアルゴリズム講座】
— 因幡めぐる@競技プログラミング (@meguru_comp) February 9, 2016
二分探索(整数)の書き方
難しさ:4 pic.twitter.com/LGLbkS0D7l
これをベースにやっていきます。
まず、めぐる式二分探索とは、次のような実装です。
long ok = 0, ng = x;
while (1 < abs(ok-ng)) {
long mid = (ok+ng) / 2;
if (f(mid)) {
ok = mid;
}
else {
ng = mid;
}
}
この実装では、whileの条件式が1 < abs(ok-ng)になっています。
このおかげで、okとngの大小関係に気を配らなくてよくなります。
関数$f$の実装と二分探索のアルゴリズム部分を分けているのも特徴的です。 これによって、
- 初期値
ok及びngの設定 - 関数$f$の内部実装
さえきちんとできていれば、あとはボイラープレートとして扱えるという利点があります。 基本はこれ一本ですべてうまくいきます。
ということで、ここからは関数$f$の設計と初期値の設定に注力しましょう。
関数$f$の設計
関数の設計は、二分探索で最も重要な部分です。 ここをミスったらどうやってもバグります。
関数の設計で気を付けることはただ一つです。
必ず$f(x)=0$及び$f(y)=1$なる$x$、$y$が存在するようにしてください。
当たり前だろ。と思った方、意外にも見落とすことがあるので、本当に気を付けたほうがいいです。 配列の探索や、ちょっと変則的な関数から$f$を作る場合、定義域が知らぬ間に制限されることがあります。
このような場合、定義域の外まで定義域を拡張して回避するテクニックがあります。あとで触れます。
初期値の設定
初期値の設定は、$f$をうまく構成できたことを確認してから行いましょう。 初期値の設定に落とし穴は少ないです。
okが区間のどちら側か?- $f$の中で計算するとき、
ok、ngはオーバーフローしないか? - 本当に$f(\mathrm{ok}) \neq f(\mathrm{ng})$が成立しているか?(もっと初期値を大きく/小さくとる必要があるか?)
あたりを調べれば、経験上大体うまくいきます。
練習問題
いくつか練習問題を用意しました。 要は習うより慣れろってことです。
解説も用意してみました。ぜひ見てみてください。
Q1: 年齢あてゲーム
問題
あなたは相手に、「年齢は$x$歳以上ですか?」と何回でも質問できます。 なるべく少ない回数で年齢を当てましょう。
制約
- $0 \leq (相手の年齢) \leq 10^{18}$
解答
$$ \begin{equation*} f(x) = \begin{cases} 1 & \text{if ($x$に対する質問の答えがYes),} \\ 0 & \text{if ($x$に対する質問の答えがNo).} \end{cases} \end{equation*} $$
とすれば、$f$として満たすべき性質を満足します。 よって、次のような解答ができます。
bool f (long x) {
return ask(x); // ask: long -> bool を暗黙に仮定
}
long ok = 0, ng = 10L^^18+1;
while (1 < abs(ok-ng)) {
long mid = (ok+ng) / 2;
if (f(mid)) {
ok = mid;
}
else {
ng = mid;
}
}
writeln("age = ", ok);
図にするとこうです。
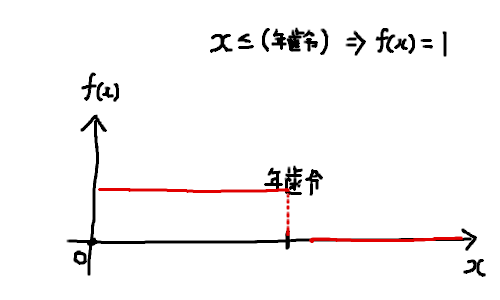
- ポイント: $f$の構成は簡単ですが、
okを左端にすること、ngの初期値に注意が必要です。
Q2: LowerBound
問題
$N$要素の配列$A$が与えられる。ここで、$i < j \Rightarrow A[i] < A[j]$が保証される。 $A$の要素であって、$x$以上のものの集合$B$を考える。すなわち、$B = \{a \in A | x \leq a \}$である。 $B$の最小要素を求めよ。$B = \emptyset$である場合はその旨を報告せよ。
制約
- $1 \leq N \leq 2 \times 10^5$
- $0 \leq i \leq N-1$に対して、$-10^9 \leq A[i] \leq 10^9$
- $-10^9 \leq x \leq 10^9$
解答
$$ \begin{equation*} f(i) = \begin{cases} 0 & \text{if $i < 0$,} \\ 0 & \text{if $A[i] < x$,} \\ 1 & \text{if $x \leq A[i]$,} \\ 1 & \text{if $N \leq i$.} \\ \end{cases} \end{equation*} $$
と定めれば、二分探索に使える関数になります。 範囲外参照をしている場合は右側にはみ出していれば$1$とし、左側にはみ出している場合は$0$としています。
この関数を用いて二分探索することで、$x \leq A[i]$なる最小の$i$を見つけることができます。 $i = N$であれば$B = \emptyset$を判定できます。
なぜ範囲外に対しても値を定義しているかというと、$A$の要素がすべて$x$未満であったり、すべて$x$以上であることがあり得るからです。 この工夫をしないと、変な場合分けをする必要が出てきます。
bool f (int i) {
if (i < 0) return false;
if (N <= i) return true;
return x <= A[i];
}
int ok = N, ng = -1;
while (1 < abs(ok-ng)) {
int mid = (ok+ng) / 2;
if (f(mid)) {
ok = mid;
}
else {
ng = mid;
}
}
if (ok == N) {
writeln("B is empty");
}
else {
writeln(A[ok]);
}
図にするとこんな感じです。
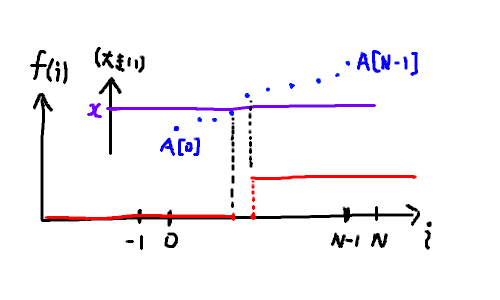
Q3 (Advanced Problem): ABC309C - Medicine
問題
高橋君は医者のすぬけ君から$N$種類の薬を処方されました。$i$種類目の薬は(処方された日を含めて)$a_i$日間、毎日$b_i$錠ずつ飲む必要があります。また、高橋君はこれ以外の薬を飲む必要がありません。
薬を処方された日を$1$日目とします。$1$日目以降で、初めて高橋君がその日に飲む必要がある薬が$K$錠以下になるのは何日目かを求めてください。
制約
- $1 \leq N \leq 3 \times 10^5$
- $0 \leq K \leq 10^9$
- $1 \leq a_i, b_i \leq 10^9$
出典: AtCoder Beginner Contest 309 - C
この問題は二分探索に帰着するまでに考察が必要です。 頭の体操のつもりで考えてみましょう! (解けなくても心配しないでください。問題を楽しみましょう!)
解答
$x$日目に処方される薬の数は、 $$ \sum_{\substack{1 \leq i \leq N \\ x \leq a_i}} b_i $$ で求めることができます。 プログラム的には、
long sum = 0;
for (int i = 0; i < N; i++) {
if (x <= A[i]) sum += B[i];
}
という感じです。
制約から、この値は$x=1$の時最大値をとり、そこから広義単調減少することがわかります。 この性質から、この値が$K$以下になるか?を判定する関数$f$が二分探索の条件を満たしそうだと分かります。
また、$s(x)$を計算するのに$O(N)$しか必要としないため、これまた二分探索で解けそうな雰囲気があります。
結論から言うと、次の関数を用いることで二分探索可能になります。
$$ s(x) \coloneqq \sum_{\substack{1 \leq i \leq N \\ x \leq a_i}} b_i $$ とするとき、 $$ \begin{equation*} f(x) = \begin{cases} 0 & \text{if $K < s(x)$,} \\ 1 & \text{if $s(x) \leq K$.} \\ \end{cases} \end{equation*} $$
解答は以下の通りです。
import std;
import core.stdc.stdio;
void main () {
/* 入力 */
int N, K; scanf("%d%d", &N, &K);
int[] a = new int[](N);
int[] b = new int[](N);
for (int i = 0; i < N; i++) scanf("%d%d", &a[i], &b[i]);
/* sの定義 */
long s (int x) {
long ret = 0;
for (int i = 0; i < N; i++) if (x <= a[i]) ret += b[i];
return ret;
}
/* fの定義 */
bool f (int x) {
return s(x) <= K;
}
int ok = 10^^9+1, ng = 0;
while (1 < abs(ok-ng)) {
int mid = (ok+ng) / 2;
if (f(mid)) {
ok = mid;
}
else {
ng = mid;
}
}
writeln(ok);
}
時間計算量は$O(N \log{(\max{a_i})})$になります。 また、この問題は二分探索以外の解法もあります。
Q4 (Advanced Problem): ABC312C - Invisible Hand
問題
りんご市場に$N$人の売り手と $M$人の買い手がいます。
$i$番目の売り手は、 $A_i$円以上でならりんごを売ってもよいと考えています。
$i$番目の買い手は、 $B_i$円以下でならりんごを買ってもよいと考えています。
次の条件を満たすような最小の整数 $X$を求めてください。
条件:りんごを $X$円で売ってもよいと考える売り手の人数が、りんごを $X$円で買ってもよいと考える買い手の人数以上である。
制約
- $1 \leq N, M \leq 2 \times 10^5$
- $1 \leq A_i, B_i \leq 10^9$
出典: AtCoder Beginner Contest 312 - C
こちらもAtCoderから引っ張ってきました。 ちなみに私はこの問題の読解で詰まって本番で苦しみまくりました。
解答
りんごを$X$円で売ってよいと考える売り手の人数$P(X)$は、次のように求められます。 $$ P(X) = \sum_{\substack{1 \leq i \leq N \\\\ A_i \leq X}} 1 $$ りんごを$X$円で買ってよいと考える買い手の人数$Q(X)$は、次のように求められます。 $$ Q(X) = \sum_{\substack{1 \leq i \leq M \\\\ X \leq B_i}} 1 $$問題は、$Q(X) \leq P(X)$を満たす最小の$X$を求めよというものです。 ここで、$P(X)$、$Q(X)$の性質を利用します。
$P(X)$は、$X$に対して広義単調増加し、$Q(X)$は広義単調減少することがわかります。 すなわち、不等式$Q(X) \leq P(X)$はある値を境目に「それ以上なら常に成立」、「それ未満なら常に不成立」となることがわかります。
これらの考察から、二分探索できそうな感じがします。
実際に$P(X)$及び$Q(X)$を1回求めるのに$O(N)$時間しか必要としないため、うまくいきそうです!
解答例を示します。
import std;
import core.stdc.stdio;
void main () {
/* 入力を受け取る */
int N, M; scanf("%d%d", &N, &M);
int[] A = new int[](N);
int[] B = new int[](M);
for (int i = 0; i < N; i++) scanf("%d", &A[i]);
for (int i = 0; i < M; i++) scanf("%d", &B[i]);
/* P(X) */
int P (int X) {
int ret = 0;
for (int i = 0; i < N; i++) if (A[i] <= X) ret++;
return ret;
}
/* Q(X) */
int Q (int X) {
int ret = 0;
for (int i = 0; i < M; i++) if (X <= B[i]) ret++;
return ret;
}
/* f(X) */
bool f (int X) {
return Q(X) <= P(X);
}
int ok = 10^^9+1, ng = 0;
while (1 < abs(ok-ng)) {
int mid = (ok+ng) / 2;
if (f(mid)) {
ok = mid;
}
else {
ng = mid;
}
}
writeln(ok);
}
時間計算量は$O(N \log{(\max{(\max{A}, \max{B})})})$となります。
解きなおしてるときにまたWA出してしまった… この問題苦手です。
終わりに
これで記事はおしまいです。 ここまで読んでいただきありがとうございました。
二分探索は、(最近は比較的マシになってきましたが)私がずっっっっと苦手としているアルゴリズムで、いつか自分の理解をまとめたいと思っていました。 良い機会だと思って思い切って書いてみましたが、正直うまくまとめられなかった感を感じています。
もし本記事を読んで、「全然わからん!」と思った方がいれば、多分私の理解や説明が甘いせいです。すみません。 一方で、もし誰かの理解の助けになればうれしいです。
もし本記事に指摘、感想等いただけるなら、 Twitter の方までお願いします。
明日(12月7日)はみのさんによる、「2023年度財政状況報告」と、あかあくさんによる「アニメオタクのためのサイトを作った」です。 興味深いタイトルですね。 更新が楽しみです。
それではよい二分探索ライフを!