最近知ったスライド最小値関連のアルゴリズムをご紹介

はじめに

本エントリは 電通大プログラミング教室 Advent Calendar 2025 の13日目です。

昨日はChiharuさんの「言語相対論・言語としてのプログラミング言語」でした。 私は趣味でゆる言語学ラジオというyoutubeチャンネルをよく視聴しているのですが、

言語とは、ある共同体が使っている言葉の集まりです。そして言葉とは、境界線のない世界に線を引くものです。

という文章をみて、以下の動画を思い出しました。

実際Chiharuさんの指摘は私の肌感覚としても感じます。 私はC言語からプログラミングを学習し始めたので、プログラムを書くときは（無意識ですが）常にC言語の構文、仕様に沿った世界でものを見ているフシがあります。 そのためjavascriptのPromiseやそれに伴うthen、async、awaitなどの理解にはとても苦しんだ覚えがあります。 あと、twitterで一度「関数型言語をやることで思考方法が変化する」みたいな話を見たことがあります。 元ツイは忘れましたが、その方が書いたspeakerdeckはありました。

https://speakerdeck.com/naoya/guan-shu-xing-puroguramingutoxing-sisutemunomentarumoderu

振り返りはこのあたりにして、内容に入っていきます。

今日紹介すること

今日は私が最近学んだ「スライド最小値」というアルゴリズムを中心に、その応用で解ける問題、似た感じのアルゴリズムをごちゃまぜにして紹介します。 全部をまとめてうまく抽象化しているというわけではないですが、見た目が全然異なる問題に適用出来て面白いので、興味のある部分だけでも見てもらえたらと思います。

スライド最小値（最大値）

次の問題を解きます。

長さ$N$の数列$A = (A _ 0, A _ 1, \dots, {A _ N - 1})$が与えられる。 $i$個目が$[l _ i, r _ i)$であるような$Q$個の右半開区間に対して、それぞれ$\displaystyle \min _ {l _ i \leq j < r _ i}(A _ j)$を求めよ。 ただし、与えられる区間は「単調増加」するとする。すなわち、$i < j$ならば$l _ i \leq l _ j$かつ$r _ i \leq r _ j$である。

与えられる区間の単調増加制約が無い場合、この問題は（staticな）Range Minimum Queryと呼ばれる問題であり、様々な解法があります。 解法の例

単調増加制約がある場合は、スライド最小値のアルゴリズムにより$\Theta (N + Q)$時間、空間$\Theta (N)$で解けて、これは他の大体のアルゴリズムよりも優れています。 一応この問題に関しては線形RMQと呼ばれる完全上位互換が存在しますが、中身が全く異なるであるため、応用を考える上ではスライド最小値にも利があります。

アイデア

図の黒枠の区間における最小値を求めたいとしましょう。 区間の単調増加制約は、黒枠の右側、左側が右にしか動かないというものです。

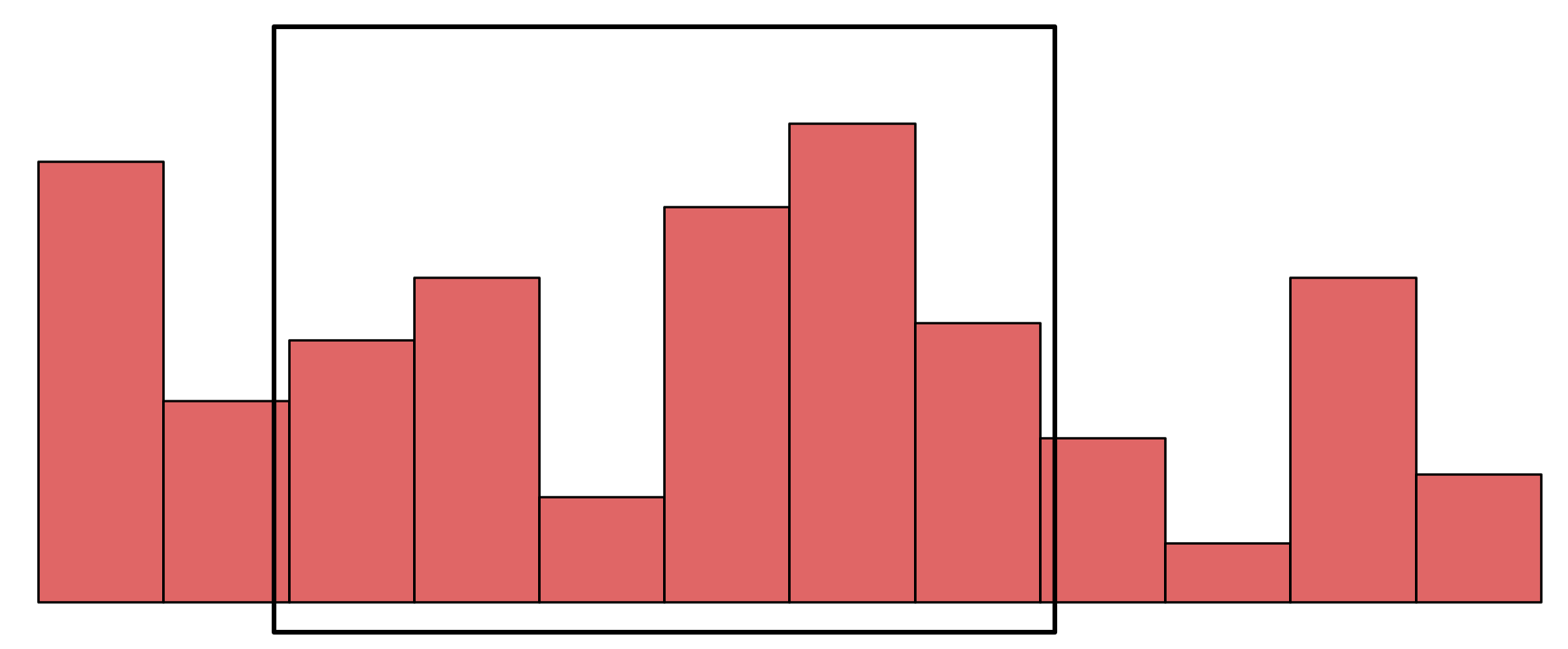
ここで、次の図の青い部分（その後ろにより小さい要素が存在する部分）について考えてみましょう。

黒枠が右方向にしかスライドしないことを踏まえると、青い部分は今回のみならず、以後もずっと最小値にはなりえないことがわかります。 なぜなら黒枠が右にスライドしたときに先に退場するのは青い部分だからです。

この部分がキモなのでもう少しかみ砕いた説明をします。 黒枠内の最初の2つの青と、その右にある赤に着目してみます。 黒枠が右にスライドしていくとき、赤要素よりも青要素の方が先に区間の外に出ることがわかります。 したがって、赤い部分が本当に最小値となるかはわからないものの、青い部分は確実に最小値となることはありえないと言えます。

よって、図の黒枠は6要素を含んでいますが、実は赤い部分の情報だけ保持していればよいということになります。

次に、右端だけが1スライドしたらどうなるのかを見てみましょう。下図は色分けを変えずに右端を伸ばしたものです。

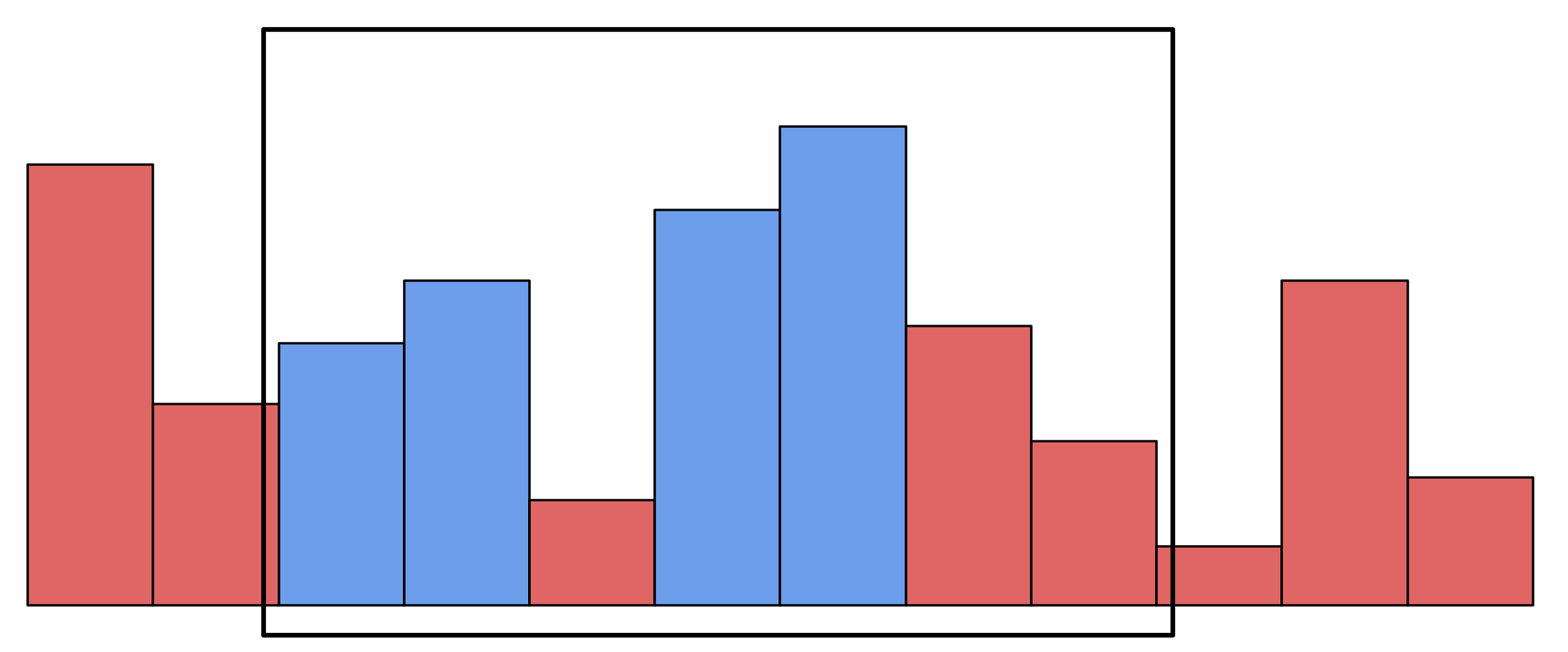
この時、新しく区間に入ってきた要素が元々の右端の要素よりも小さいため、元々の右端の要素が青色に格下げされます。（図では新しく青色になる要素を緑色で表示しています。） 左から3番目の赤色よりは大きいため、こちらは格下げされずに済みました。

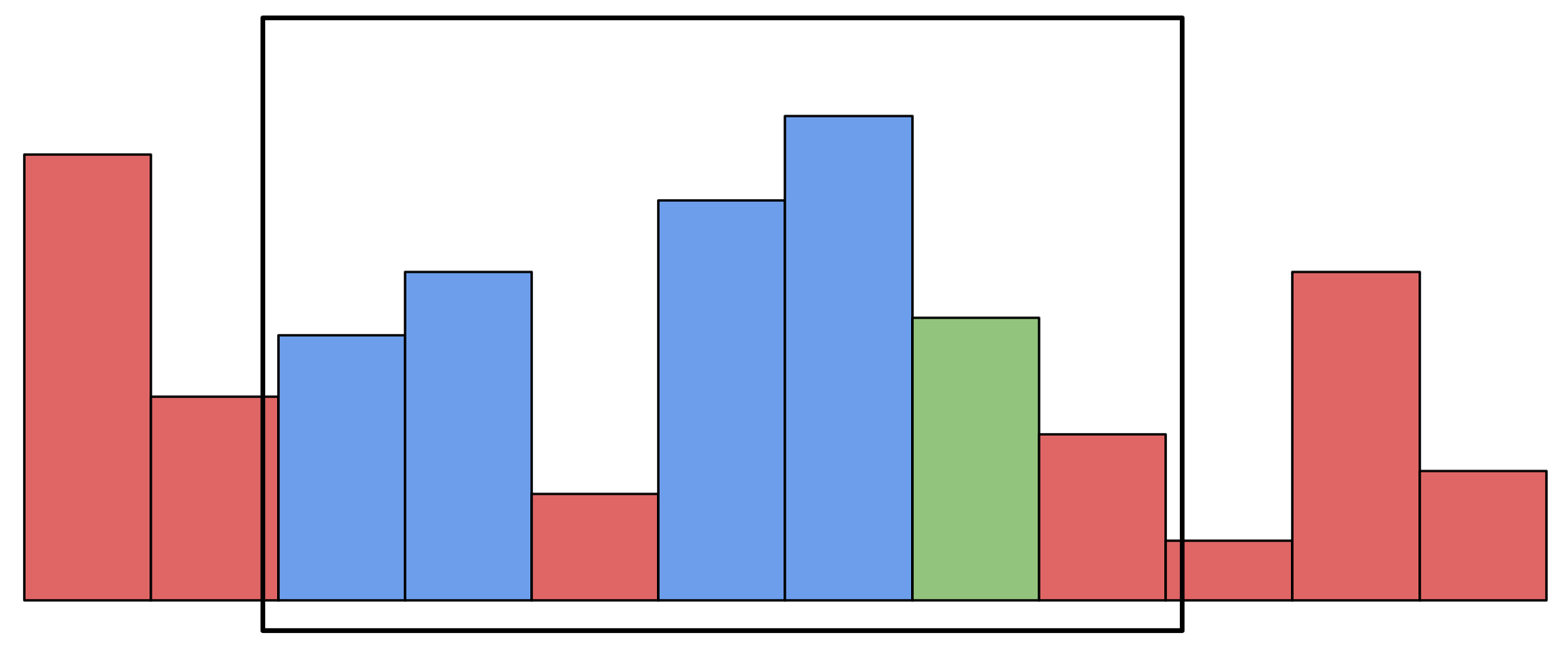
青色の定義が「区間内のより右側に自分以下の要素が存在するか」であるため、区間内の赤色のデータのみを抜き取って並べると常に単調増加になります。 また、青色は解になりえない要素で、赤色は解になりえる要素なのでした。 したがって、赤色のうち最も左にあるものが区間最小値であることが言えます。

アルゴリズム

両端キューを用いて区間内の赤色要素を管理します。 具体的には、両端キューの奥に左側の要素のインデックスが、両端キューの手前に右側の要素のインデックスが来るように管理します。 区間$[l _ i, r _ i)$に対する問題を解くときは次のようにすればよいです。

1. $r _ {i - 1} \leq x < r _ i$に対して小さいものから順に次を行う。
   1. 両端キューの先頭要素を$t$とする。$A _ t$と$A _ x$を比較し、$A _ x$以上であれば先頭要素をポップするということを繰り返す。
   2. 両端キューが空になるか$A _ t$が$A _ x$未満になったら$x$を両端キューに入れる。
2. $l _ {i - 1} \leq x < l _ i$に対して小さいものから順に次を行う。
   1. 末尾要素を$t$とする。$t = x$であれば末尾要素をポップするということを繰り返す。

これらを行った後、両端キューの末尾要素が区間最小値である。

プログラム的には次のような感じになります。

// 最初は区間[0, 0)の管理をしていると考える
int L = 0, R = 0;

// Qクエリに対して解答
for (int i = 0; i < Q; i++) {

    // ステップ1
    while (R < r[i]) {
        while (!st.empty() && A[R] <= A[st.front()]) {
            st.removeFront();
        }
        st.insertFront(R);
        r++;
    }

    // ステップ2
    while (L < l[i]) {
        if (st.back() == L) {
            st.removeBack();
        }
        L++;
    }

    // 解を記録
    ans[i] = st.back();
}

適用例

あまりスライド最小値がそのまま使える問題が見つからなかったので、少しわかりにくい例です。 ABC352D - Permutation Subsequence

$\lbrace a, a + 1, a + 2, \dots, a + K - 1 \rbrace$の方を固定して考える感じです。 $Q _ i \coloneqq iがある場所$としたとき、$\displaystyle \max _ {a \leq i < a + K} Q _ i - \min _ {a \leq i < a + K} Q _ i$を考えると良くて、この値の最小が解になります。 実際に$Q$を作り、これに対してスライド最小値とスライド最大値を適用すると$\Theta (N)$時間で解けます。

解答例

一番近い自分より小さいやつ

ふざけた名前ですいません。（いい名前が思い浮かばない。） 次の問題を考えます。

長さ$N$の数列$A = (A _ 0, A _ 1, \dots, A _ {N - 1})$が与えられる。 $0 \leq i < N$それぞれに対して、$i < j$かつ$A _ j < A _ i$となるような$j$のうち、最小のものを求めよ。

これを$\Theta (N)$時間で解きます。

アイデア

スライド最小値をベースに考えます。 区間の左側が動かないとして、右側だけ伸ばしていくときのアルゴリズムの動作を考えます。 このとき、ある$i$に対して求める$j$は、場所$i$にある要素をはじめて青くさせるような要素の場所になります。 （青く塗られた要素の定義が「区間内で右により小さい要素が存在するようなもの」だったことを思い出してください。）

したがって、青く塗るタイミングでその原因になった要素の場所をメモしていけばよいです。

アルゴリズム

同様に両端キューを使いますが、若干違う動きをします。

長さ$N$の配列$\mathrm{ans}$を用意しておく。 $0 \leq x < N$に対して小さいものから順に次を行う。

1. 両端キューの先頭要素を$t$とする。$A _ t$と$A _ x$を比較し、$A _ x$以上であれば$\mathrm{ans}[t]$に$x$を代入してから先頭要素をポップするということを繰り返す。
2. 両端キューが空になるか$A _ t$が$A _ x$未満になったら$x$を両端キューに入れる。

終了後、$\mathrm{ans}[i]$は$i$に対する解である。代入されなかった場合は解が存在しない。

プログラム的には次のようになります。

auto ans = new int[](N);
auto st = DList!(int)();
foreach (i; 0 .. N) {
    while (!st.empty() && A[i] < A[st.front()]) {
        ans[st.front()] = i;
        st.removeFront();
    }
    st.insertFront(i);
}

ヒストグラム中の最大長方形

次の問題を考えます。

長さ$N$の数列$A = (A _ 0, A _ 1, \dots, A _ {N - 1})$が与えられる。$A$をヒストグラムとしてみたとき、ヒストグラム中の面積が最大の長方形を求めよ。

つまりこういうことです。

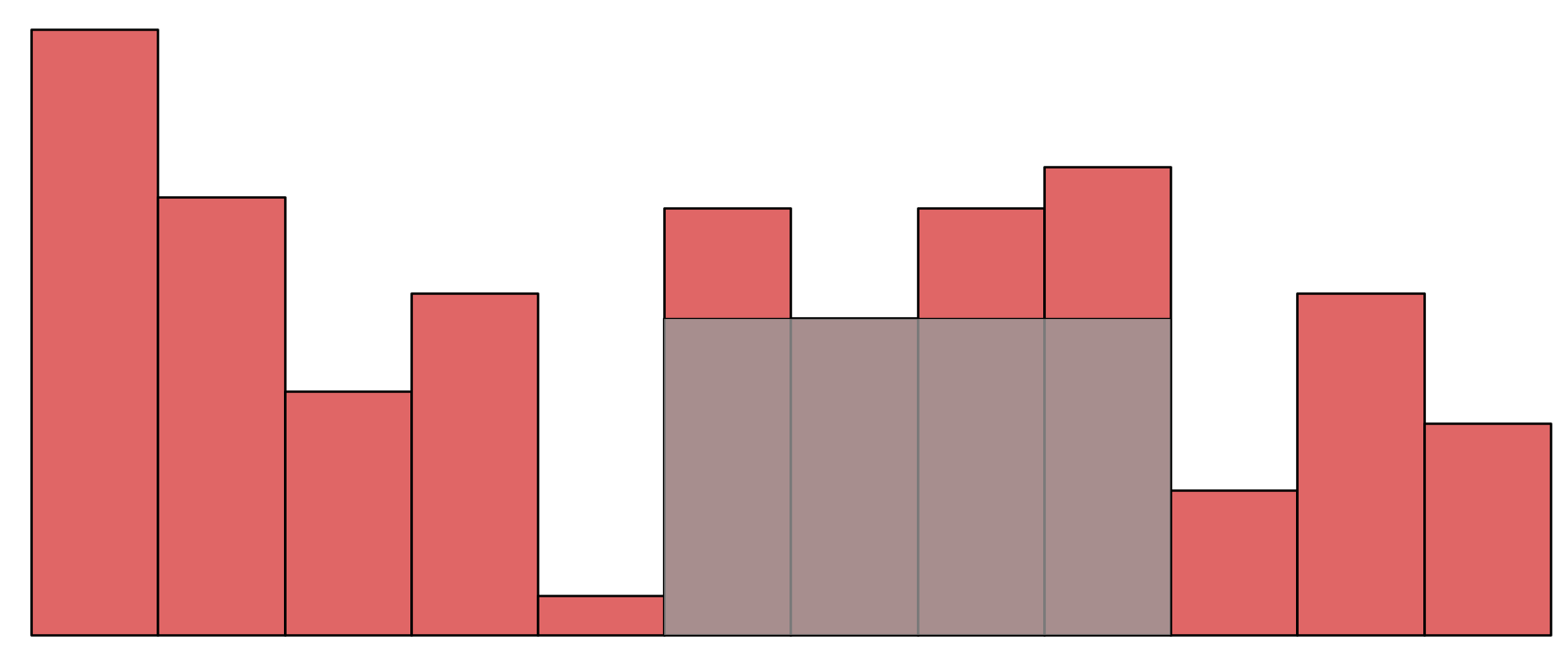
アイデア

長方形の横幅が$i$番目から$j$番目であるとき、長方形の縦幅は$\displaystyle \min _ {i \leq x \leq j}(A _ x)$になります。 なぜなら、それより大きければ上側にはみ出してしまうし、それより小さければ明らかに面積最大でないからです。

つまり、面積最大となる長方形は必ず上面がどこかにぴったりくっついていることになります。 では、逆に高さが$A _ i$であるような長方形が左右にどこまで伸ばせるのかがわかれば、これを各$i$について考えたときの最大値が解になるはずです。

ここで、左右にどこまで伸ばせるかは$i$と一番近い$A _ i$より小さい要素がどこにあるかに依存します。 そのような場所を探す方法はすでに前節で説明しましたね。

前処理に$\Theta (N)$時間、本処理に$\Theta (N)$時間かかるので全体$\Theta (N)$時間で解けます。

アルゴリズム

前章で紹介した方法を用いて、$0 \leq i < N$それぞれに対して、

1. $i < j$かつ$A _ j < A _ i$なる$j$のうち最小のもの
2. $j < i$かつ$A _ j < A _ i$なる$j$のうち最大のもの

を求める。 これらを用いて、各$i$について、高さが$A _ i$であり、$i$から左右に伸ばしたときの最大長方形を求める。 その最大値が解である。

verify

同じ問題がAOJに公開されています。 ヒストグラムの中の最大長方形

解答例

最大長方形問題

次の問題を考えます。

正方形のタイルが縦$H$個、横$W$個並べられている。 タイルは白色か黒色であり、上から$i + 1$個目、左から$j + 1$個目のタイルの色は$c _ {i, j}$で表される。 白色のタイルの実を含む最大の長方形を求めよ。

つまりこういうことです。

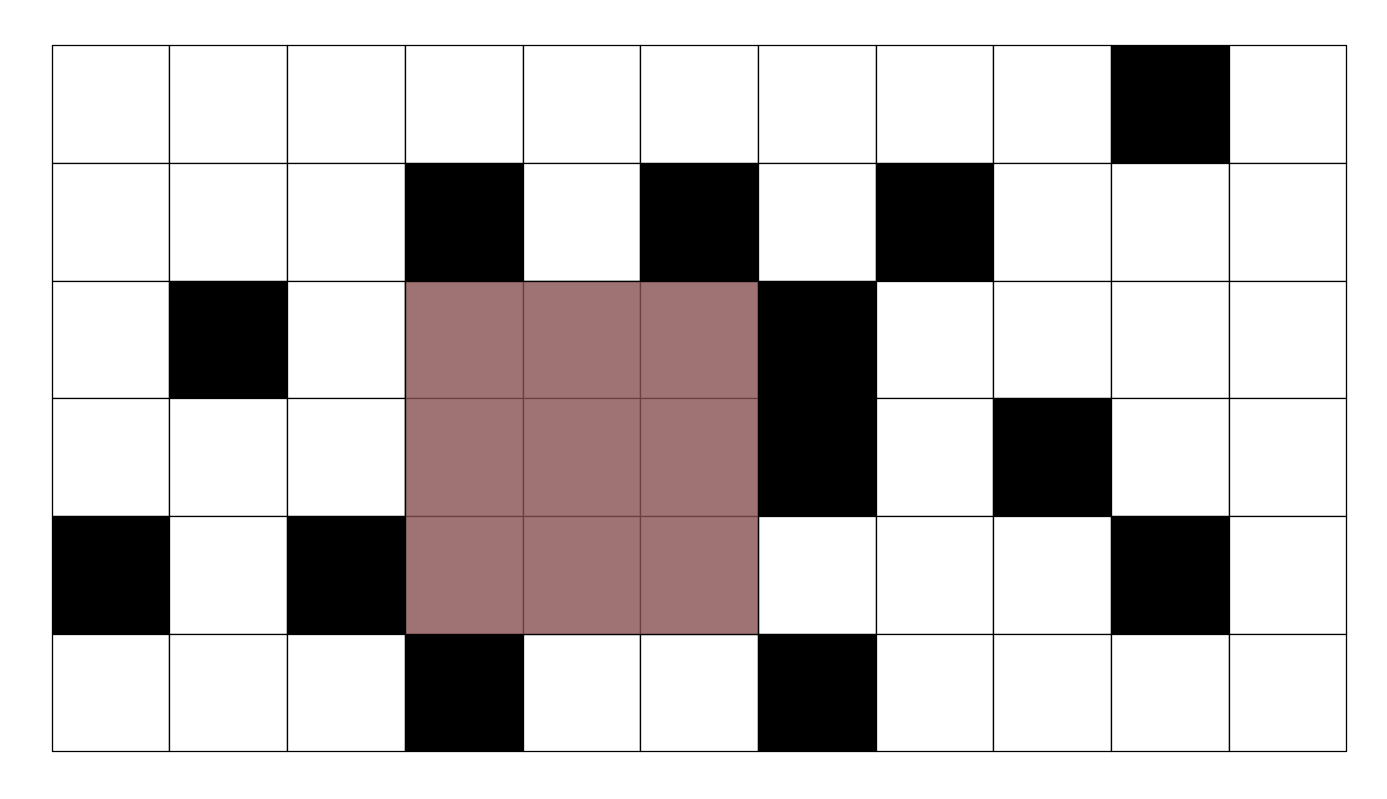
アイデア

長方形の底辺を固定して考えてみます。 例えば例として下から3個目のマスが底になるようにしてみましょう。わかりやすいように赤線を引きました。

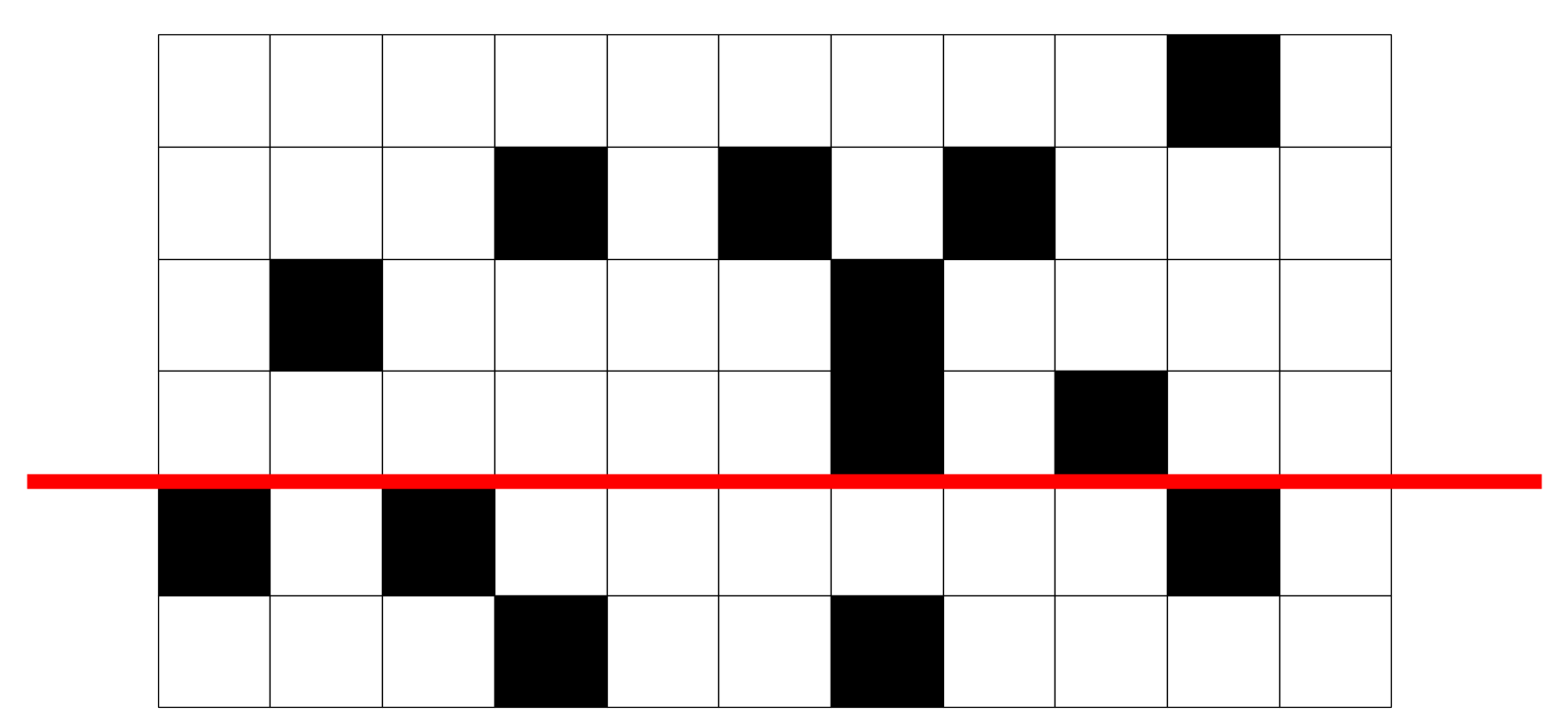
長方形は黒マスを含まないことを考えると、赤線より上にある黒マスすべてについて、その上にあるマスを含むような長方形はありえません。逆に、それ以外のマスならば、それを含む長方形が少なくとも1つ以上存在します。 使えるマスを青色に塗った図を以下に示します。

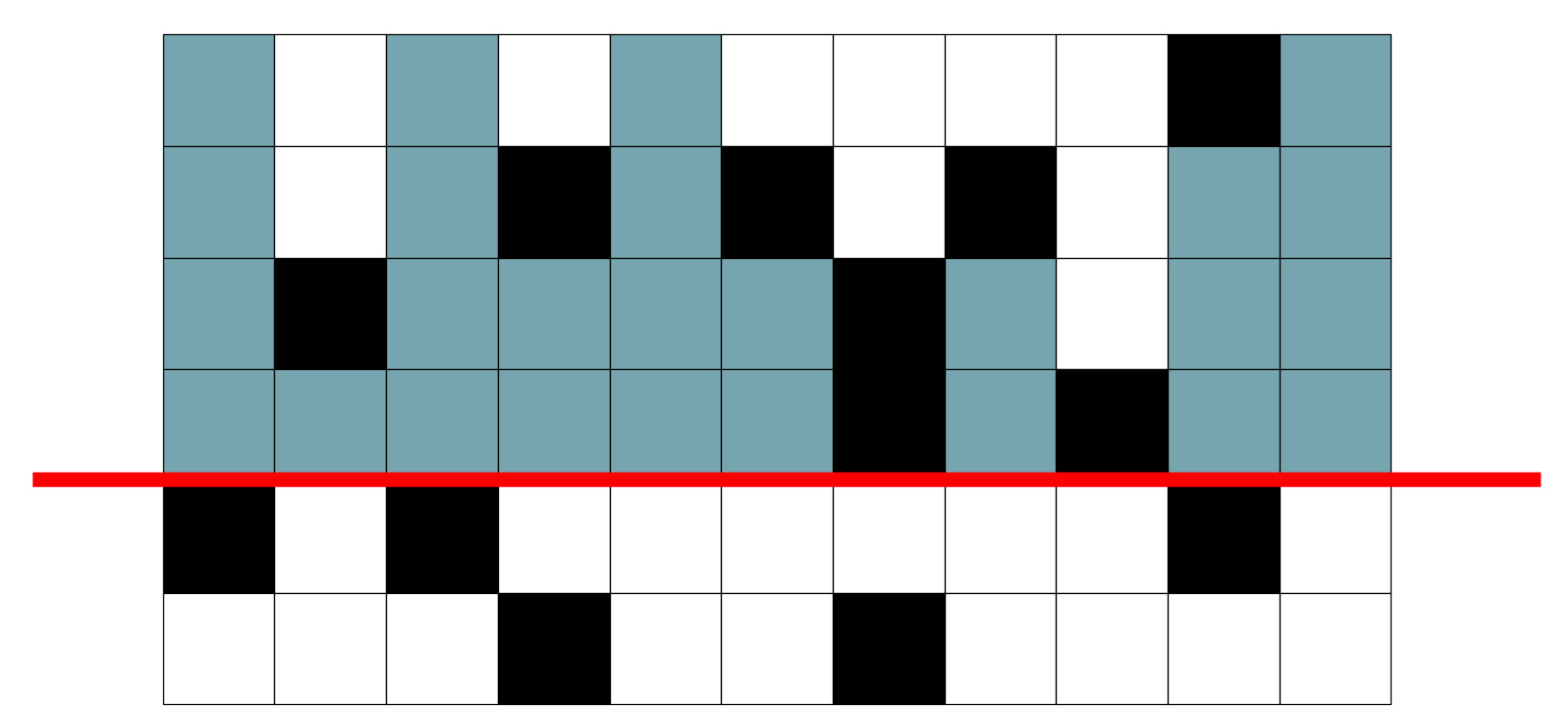
この青色のマスの中から面積最大の長方形を見つければよいことがわかりました。

ところで、よくみると青マスの集合はヒストグラムになっています。 これはたまたまではありません。 使えるマスの条件を考えると、各列の使えるマスは連結になるため、常にヒストグラムになります。

そこで、前節で紹介したヒストグラム中の最大長方形アルゴリズムを適用することで$\Theta (W)$時間で解くことができます。 これを各行について行えばよいため、全体$\Theta (HW)$時間で解くことができます。

アルゴリズム

ヒストグラム中の最大長方形アルゴリズムに帰着しやすいよう工夫します。

1. 各列に対して、黒マスが来たらリセットという感じで番号を振る。ただし黒マスは0を振る。（下図参照）
2. 各行に対して、振られた番号を抜き出してヒストグラムの最大長方形アルゴリズムを適用する。これらの最大値が解である。

verify

同じ問題がAOJに公開されています。 最大長方形

解答例

おわりに

書くの疲れました。 スタックがすごいのかminやmaxの成す代数構造がすごいのかよくわからないけど、いろいろできるみたいです。 特に、最大長方形問題への帰着はわかれば当たり前ですが、最初なるほどな～と思いました。 他にもカルテシアンツリーの構築にも役に立つらしいです。疲れたので調べていません。

あとは関連アルゴリズムとして、グリッド上の最大正方形問題、Sliding Window Aggregation（SWAG）と呼ばれるデータ構造について紹介しようと思っていたのですが、こちらもやはり疲れたのでやめます。

明日はまだ埋まっていないみたいなのでヒマな人は是非やってみてください。 マジで誰もいなければ何か書こうかな。