MMA Contest 015 参加記録
Published on 2023-06-01Last Modified 2023-06-01
Table Of Contents
はじめてのオンサイト、行ってキタ!
電気通信大学にはMMAという格闘技みたいな名前のサークルがあります。
先日2023年5月28日、そのサークルの有志がオンサイトコンテストを開いていたので、(ヒマなので)参加してきました!
MMA Contest 015というオンサイト競技プログラミングコンテストを開催します!
— 電気通信大学 MMA (@uecmma) May 8, 2023
大学HPにもリンクを貼ってもらうことができました���
教室は200人が余裕で入る教室のB202で実施します。
まだまだ参加枠に余裕があるので、参加登録お待ちしております!https://t.co/Jrqil1Yvpg
明日,東京都調布市にある電通大でレート不問初中級者向け予選なし誰でも来てくれオンサイトコンテストを開催します!
— Nafmo@固定イベント (@Nafmo2) May 27, 2023
コンテストページはYukicoderを使います.まだ間に合うので明日あいていればお越しください~https://t.co/0lkHO7Xeb8
参加した感想(?)
コンテストが行われた教室は、電気通信大学の中でもかなり大きい方の教室だったのですが、思っていたよりもたくさん人がいてびっくりしました。 また、僕よりも若い方から社会人の方まで様々な方がいらっしゃったそうです。 すごい非日常感で面白かったです。(小並感)
その日にARCがあるということと、参加者に知り合いが一人もいないという事情から終了後即帰ってしまったので、 他の方がどのような交流をしていたのかよくわかっていませんが、とても楽しそうな雰囲気でした。

↑ココです。
初心者向けコンテストと謳っていたものの、私にとって難しい問題が多く、良い練習になりました。 運が良かったのか、12問中5問正解することができ、全体83位で終わりました。 2時間を超えるコンテストは初めてだったので、結構疲れました。
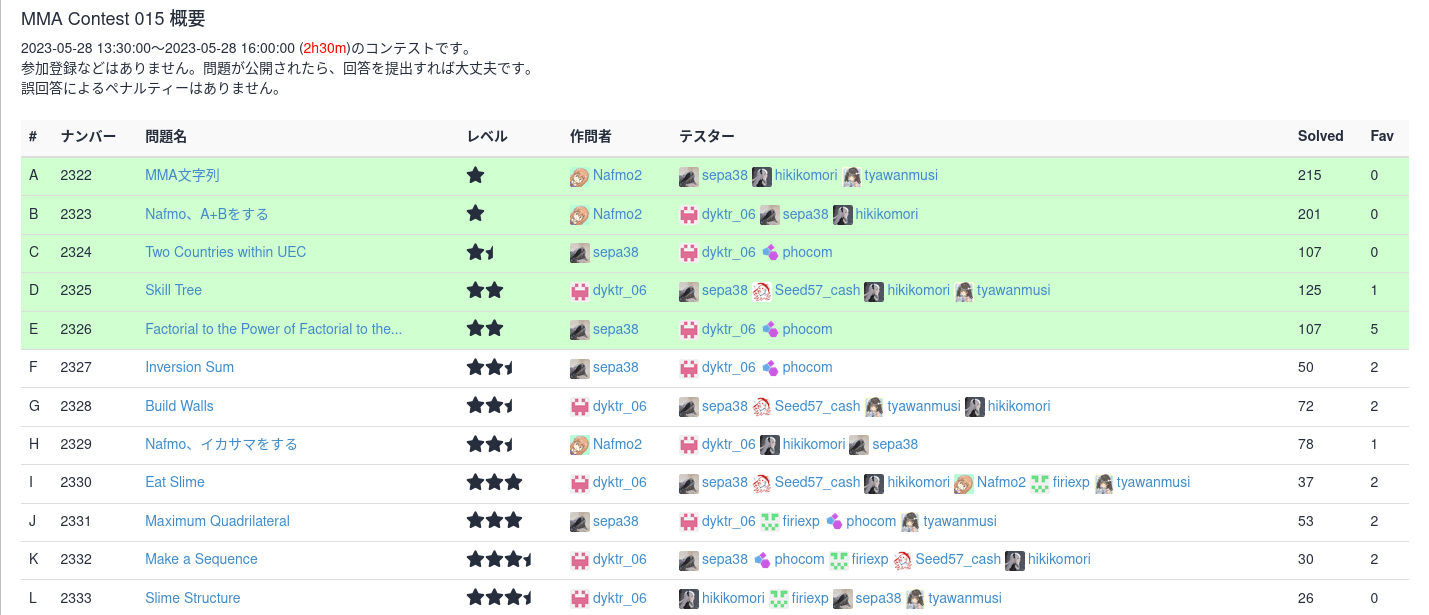

解けた問題の概要と解法
自分が解けた問題をてきとーに振り返ります。
A - MMA文字列
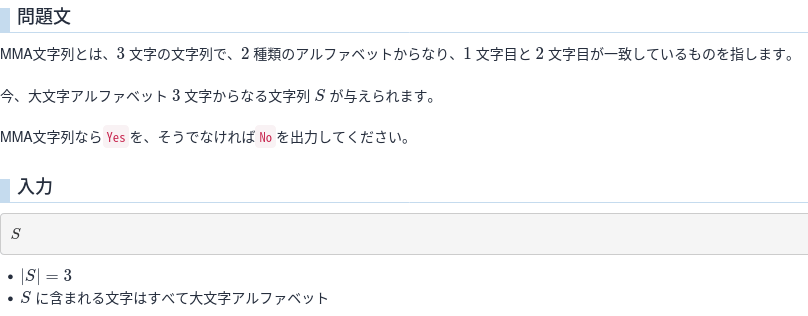
コンテストが始まった瞬間から会場中「カタカタ…」という音が響きだし、結構焦りながら解きました。
シンプルな問題ですが、S[0] == S[1] && S[1] == S[2]というケースが意外と落とし穴になっています。(1WA)
B - Nafmo、A+Bをする
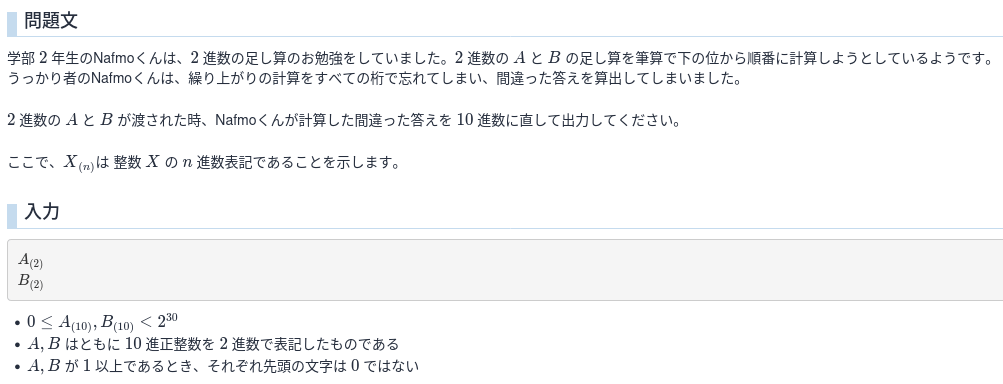
繰り上がりをしない2進数の足し算です。
私は配列に値を入れて、XOR演算(片方が1、片方が0のときのみ1)をシミュレートする感じで解きました。
注意点としては、文字列Sをbit列と見立てたとき、S[0]はその見た目に反して最上位bitになります。
AtCoderのコンテストの方でこれに気づかずに一生WAしていたことがあるので、今回はしっかり対応できました。
C - Two Countries within UEC
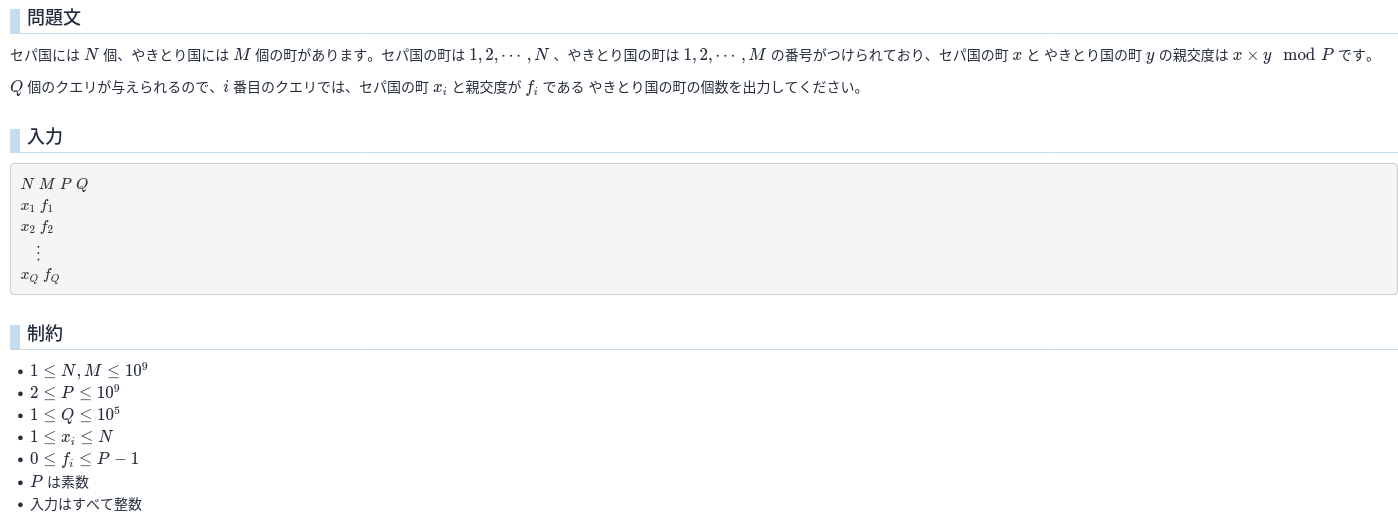
作問のsepa_38さん曰く、「皆さんにWAをお配りするために作りました」だそうです。 クソむずかった…
はじめはC問題ということもあって、ちょっと考えたら解けるだろう!と思って考察していました。
実際、$f$が$x$の倍数であるときにはシンプルになります。 この問題を言い換えると、「xが与えられる。法をPとして$xy=f$であるようなyの個数を求めよ」となるので、 前述のようなケースでは法をPとしてy=f/xであるようなyを求めるだけです。 これは割り算ですぐできます。
しかし、その他のケースについてはどうしても難しいです。 上の条件を更に噛み砕くと、「$x$、$f$が与えられる。ある(0を含む)自然数$k$が存在して、$xy=f+kP$が成立するような$y$を数え上げよ」 という問題になります。 これを変形していって、「$y=(f+kP)/x$が成立するような$(k, y)$の組を数え上げよ」とまで持っていきました。
しかし、これは普通にやったらめちゃくちゃ計算量がかかります。 少なくとも私は全探索以外わかりません。
ということで、方針転換。 もしかしたら逆元というものが使えるのではないか?と考え、google先生に聞きました。
結果、$x$と$P$が互いに素であるとき、 $[0, P-1]$にただ一つの$x^{-1}$が存在して、$P$を法として$x\cdot x^{-1}=1$である。 という結果を得ました。やった!これならPを法として$y=f \cdot x^{-1}$(右辺は整数)が成立するようなyを数え上げる問題に帰着できる! ということで実装します。
とはいっても逆元なんて使ったことなく、
実装方法よく知らなかったので、ネット上に落ちてたc++のコードをD言語で動くように改造して無理やりACしました。
なんかふぇるまーのしょうていり(?)を使っているそうです(バカ)
また、$x$と$P$が互いに素でないとき、任意の$y$に対して友好度が0であることに気をつける必要があります。
modpow関数をバグらせまくってかなりペナを喰らいました。
D - Skill Tree

問題文がゴツくて一瞬ビビりましたが、理解してしまえばそこまで複雑なことを聞いていないことがわかります。 ポイントは2つです。
- ある技を覚えるために、事前に覚えておく必要のある技がある。
- ある技を覚えるために、一定のレベルに達している必要がある。
これは技を覚える順番に依存関係があるということです。 グラフ表現に落とし込むことで機械的に処理できそうな感じがしますね。
まず、有向グラフを構築します。 技一つ一つを一つのノードと見て、その技を覚えることでアンロックされる技へと有向辺を張ります。
まずは覚えられるかどうかをどう判定するか考えます。 最初に覚えているのは技1のみであるので、ある技が習得可能な必要十分条件は、 技1を含む連結成分にその技が含まれていることです。 これはdfsなどを用いて簡単に判定できます。
また、ある技を覚えるために依存している技はちょうど1つです。 つまり、技の依存関係は一本道になり、分岐しません。 この性質から、技を覚える必要コストも容易に算出できます。
(ある技を覚えるために必要なレベル)=max((それが依存している技を覚えるのに必要なレベル), (それ自身を覚えるために必要なレベル))
というように、一種の動的計画法のように計算することができます。 これでクエリ2に答える目処が立ちました。
残りはクエリ1です。 まず愚直に考えます。 これを判定するには、技1のノードから順番に技を見ていって、 初めてxを超えるコストを持つノードについたときに今までたどったノードの数を答えることで達成できます。
換言すると、「技を覚えるためのコストを昇順に並べたとき、xは列の何番目に入りますか?」というものです。 よって、配列にコストを全部入れてソート→xの入る位置を2分探索で求めるという操作で答えることができます。
計算量は言及しませんが、これで十分高速に動作し、ACが取れました。 クエリ1の解法が面白かったです。
E - Factorial to the Power of Factorial to the…
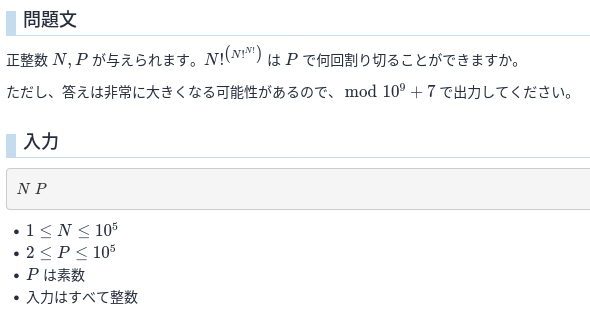
見た目がゴツい! 怖すぎる!
さて、まず指数部分がデカすぎてよくわからないので、条件を弱めた問題を考えます。
「N!はPで何回割れますか?」
という問題は典型問題で、 ルシャンドルの定理 を用いて解くことができます。 さて、残りの問題を考えましょう。
N!をx乗するとき、明らかにN!の素因数の個数はx倍になります。 (明らかにと言っていますが、私の中ではココが一番の山場かなと思います。) そこで、答えは上の問題の答えを$N!^{N!}$倍したものになります。 $N!:=N \cdot (N-1) \cdot (N-2) \cdot (N-3) … 2 \cdot 1$であるから、指数部分をほぐすことができて、
$N!^{(N!)} = N!^{(N \cdot (N-1) \cdot …2 \cdot 1)}$ $= N!^{N^{{N-1} \dots ^{2^{1}}}}$
となります。(二番目の変形は指数法則を用いています。) N乗の計算は繰り返し2乗法で高速にできるので、これで$N!^{N!}$を$O(NlogN)$で求められました。 というわけで適宜余りをとっていけばACになります。 ABCのD問題に出そう!解けてウレシイ…
終わりに
コンテスト面白かったです。また開催してほしい…
参加記録の更新をずっとサボっててごめんなさい。 更新をサボっている間にメイン言語を切り替えたり、longest streakでトップ1000に入ったり、400ACカウント達成したり、色々ありました。
最近は大半をmarkdownで書いてサボっているので、もっと更新できたらなと思います。
競技プログラミング以外の話題も書きたいとは思っているんですが、なんか面倒くさくてサボってしまいます。助けてくれ。
それでは次のエントリで。