MMA Contest 018参加記録 + 怪文書
Published on 2024-04-03Last Modified 2024-04-03
Table Of Contents
オンサイトに行ってきました。

電気通信大学のサークル、MMAによるプログラミングコンテストが3月31日に開催されました。 電気通信大学内にオンサイト会場が確保されていたため、私も現地に行って参加してきました。 本エントリはその記録になります。
戦績
8問中7問正解し、4月1日時点で全体57位でした。
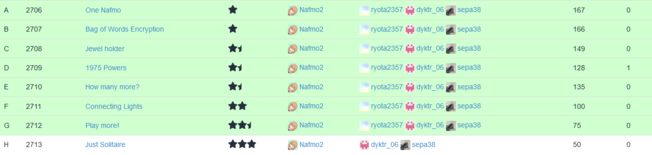
振り返り
A - One Nafmo
$A$本セットでしか買えない鉛筆をいくつか買うことで、合計$X$本以上手に入れる問題です。 早い話、$X / A$の切り上げが処理できれば良いです。 これは条件分岐などでもよいですが、次のイディオムがよく利用されています。 $$\left\lceil \frac{X}{A} \right\rceil = \left\lfloor \frac{X + A - 1}{A} \right\rfloor$$
import std;
void main () {
int A, B, X; readln.read(A, B, X);
writeln(B * ((X + A - 1) / A));
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
B - Bag of Words Encryption
文字列$S$に対して、(文字Aが登場する回数)(文字Bが登場する回数) ... (文字Zが登場する回数)という文字列を出力する問題です。
一旦配列等に各文字の出現回数を記録するときれいに解けます。
文字列として構築しなくても、整数の出力を26回行うこともできます。
import std;
void main () {
int N = readln.chomp.to!int;
string S = readln.chomp;
int[char] C;
foreach (c; S) C[c]++;
string X = "";
foreach (i; 0..26) {
X ~= C.get((i + 'A').to!char, 0).to!string;
}
writeln(X);
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
C - Jewel holder
少し複雑なグリッドの上であり得る経路数の数え上げをする問題です。 私が「グラフの多重化」と呼んでいるテクニックを用いることで、よくあるdpに帰着できます。 「グラフの多重化」とは、現在のグリッドの座標に加えて何かしらの情報を持たせることです。 今回に関しては、$\mathrm{dp}[i][j][k] \coloneqq \text{$(i, j)$にいて、宝石$k$個を持っている状態にたどり着く場合の数}$ とすることで、うまくdpができます。
import std;
void main () {
int H, W; readln.read(H, W);
auto A = new string[](H);
foreach (i; 0..H) A[i] = readln.chomp;
auto dp = new int[][][](H, W, H * W + 1);
// dp[i][j][k] := (i, j)に宝石k個で至る場合の数
dp[0][0][1] = 1;
foreach (i; 0..H) {
foreach (j; 0..W) {
foreach (k; 0..H * W + 1) {
// 右
if (i + 1 < H) {
char c = A[i + 1][j];
if (c == 'o') {
if (k < H * W) dp[i + 1][j][k + 1] += dp[i][j][k];
}
if (c == 'x') {
if (0 < k) dp[i + 1][j][k - 1] += dp[i][j][k];
}
}
// 下
if (j + 1 < W) {
char c = A[i][j + 1];
if (c == 'o') {
if (k < H * W) dp[i][j + 1][k + 1] += dp[i][j][k];
}
if (c == 'x') {
if (0 < k) dp[i][j + 1][k - 1] += dp[i][j][k];
}
}
}
}
}
long ans = 0;
foreach (k; 0..H * W + 1) {
ans += dp[H - 1][W - 1][k];
}
writeln(ans);
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
また、制約が十分小さいため、グラフの巡回路すべてを列挙することが可能なようです。各巡回路に対してはシミュレーションをすると正しく数え上げることができます。
D - 1975 Powers
条件を満たす部分列を数え上げる問題です。
部分列$(a, b, c, d)$に対して、$10^a + 9^b + 7^c + 5^d$を対応させることにします。 $A$をソートすることで、$a < b < c < d$が保証することができます。
この工夫により、取る/取らないdp(オレオレ語彙です)に帰着されます。 具体的には$\mathrm{dp}[i][j][k] \coloneqq \text{先頭$i$項から$j$項とって、現在の和のあまりが$k$}$とすることで解けます。 しかし、このままだといろいろ厳しいので、前計算でlogを落としたり、nextdpというテクニックを用いてメモリ使用量を減らしました。
import std;
void main () {
int N, P, Q; readln.read(N, P, Q);
auto A = readln.split.to!(int[]);
solve(N, P, Q, A);
}
void solve (int N, int P, int Q, int[] A) {
// なんかMLEしたのでnextdpやる
A.sort;
auto dp = new long[][](5, P);
auto ndp = new long[][](5, P);
// dp[i][j][k] := 先頭i個からj個とってあまりがk
dp[0][0] = 1;
const x = [10, 9, 7, 5];
auto memo = new long[][](4, N);
foreach (i; 0..4) foreach (j; 0..N) memo[i][j] = mod_pow(x[i], A[j], P);
foreach (i; 0..N) {
foreach (d; ndp) d[] = 0;
foreach (j; 0..5) {
foreach (k; 0..P) {
// 取る
if (j + 1 <= 4) {
ndp[j + 1][(k + memo[j][i]) % P] += dp[j][k];
}
// 取らない
ndp[j][k] += dp[j][k];
}
}
swap(dp, ndp);
}
writeln(dp[4][Q]);
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
long mod_pow (long a, long x, const long MOD)
in {
assert(0 <= x, "x must satisfy 0 <= x");
assert(1 <= MOD, "MOD must satisfy 1 <= MOD");
assert(MOD <= int.max, "MOD must satisfy MOD*MOD <= long.max");
}
do {
// normalize
a %= MOD; a += MOD; a %= MOD;
long res = 1L;
long base = a;
while (0 < x) {
if (0 < (x&1)) (res *= base) %= MOD;
(base *= base) %= MOD;
x >>= 1;
}
return res % MOD;
}
想定解はdpではなく、ギリギリの計算量につく定数倍を見極められるかというものでした。 部分列をとるときに、できる列が重複しないようインデックスを動かすことで$1/24$の定数倍をつけることができます。 このため$O(N^4)$が間に合うようになるというからくりです。
E - How many more?
一列に並んだ人の座標が与えられるので、ある2人の間にいる人の数を求める問題です。
$A$の要素は大きいものの、要素数は$N$です。また、$A$はお互いの大小関係さえわかればよいため、座標圧縮することでうまく処理できます。 二分探索等を用いる解法もありますが、座標圧縮はタイブレークの処理が非常に楽になります。
後は数列$A$の圧縮列に対してstatic range sum queryが解ければよいので、累積和やセグメントツリーを用いましょう。
import std;
void main () {
int N, Q; readln.read(N, Q);
auto A = readln.split.to!(int[]);
solve(N, Q, A);
}
void solve (int N, int Q, int[] A) {
// 座圧 + RSQ
int[int] f; // ゴールからの距離 -> 全体の順番
int[] f_inv;
{
auto B = A.dup.sort.uniq.array;
foreach (i; 0..B.length) f[B[i]] = i.to!int;
f_inv.length = f.length;
foreach (key, val; f) f_inv[val] = key;
}
auto RSQ = new SegmentTree!(int, (int a, int b) => a + b, () => 0)(N);
foreach (a; A) RSQ.set(f[a], RSQ.get(f[a]) + 1);
foreach (i; 0..Q) {
int x, y; readln.read(x, y);
x--, y--;
// A[y] < hoge < A[x]
if (f[A[x]] <= f[A[y]]) {
writeln(0);
continue;
}
writeln(RSQ.prod(f[A[y]] + 1, f[A[x]]));
}
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
import std.traits : ReturnType, isCallable, Parameters;
import std.meta : AliasSeq;
class SegmentTree (T, alias ope, alias e)
if (
isCallable!(ope)
&& isCallable!(e)
&& is (ReturnType!(ope) == T)
&& is (ReturnType!(e) == T)
&& is (Parameters!(ope) == AliasSeq!(T, T))
&& is (Parameters!(e) == AliasSeq!())
)
{
/* 内部の配列が1-indexedで2冪のセグメントツリー */
import std.format : format;
T[] X;
size_t length;
/* --- Constructors --- */
this (size_t length_) {
adjust_array_length(length_);
for (size_t i = length; i < 2*length; i++) {
X[i] = e();
}
build();
}
import std.range.primitives : isInputRange;
this (R) (R Range)
if (isInputRange!(R) && is (ElementType!(R) == T))
{
adjust_array_length(walkLength(Range));
size_t i = length;
foreach (item; Range) {
X[i] = item;
i++;
}
while (i < 2*length) { X[i] = e(); i++; }
build();
}
/* --- Functions --- */
private
void adjust_array_length (size_t length_) {
length = 1;
while (length <= length_) length *= 2;
X = new T[](2*length);
}
void set_with_no_update (size_t idx, T val)
in {
assert(idx < length,
format("In function \"set_with_no_update\", idx is out of range. (length = %s idx = %s)", length, idx));
}
do {
X[length+idx] = val;
}
void build () {
for (size_t i = length-1; 1 <= i; i--) {
X[i] = ope(X[2*i], X[2*i+1]);
}
}
public
override string toString () {
string res = "";
int level = 1;
while ((2^^(level-1)) < X.length) {
res ~= format("level: %2s | ", level);
for (size_t i = (2^^(level-1)); i < (2^^level); i++) {
res ~= format("%s%s", X[i], (i == (2^^level)-1 ? "\n" : " "));
}
level++;
}
return res;
}
void set (size_t idx, T val)
in {
assert(idx < length,
format("In function \"set\", idx is out of range. (length = %s idx = %s)", length, idx));
}
do {
idx += length;
X[idx] = val;
while (2 <= idx) {
idx /= 2;
X[idx] = ope(X[2*idx], X[2*idx+1]);
}
}
T get (size_t idx)
in {
assert(idx < length,
format("In function \"get\", idx is out of range. (length = %s idx = %s)", length, idx));
}
do {
idx += length;
return X[idx];
}
T prod (size_t l, size_t r)
in {
assert(l < length,
format("In function \"prod\", l is out of range. (length = %s l = %s)", length, l));
assert(r <= length,
format("In function \"prod\", r is out of range. (length = %s r = %s)", length, r));
assert(l <= r,
format("In function \"prod\", l < r must be satisfied. (length = %s l = %s, r = %s)", length, l, r));
}
do {
/* Returns all prod O(1) */
if (l == 0 && r == length) return X[1];
if (l == r) return e();
/* Closed interval [l, r] */
r--;
l += length, r += length;
T LeftProd, RightProd;
LeftProd = RightProd = e();
while (l <= r) {
if (l % 2 == 1) {
LeftProd = ope(LeftProd, X[l]);
l++;
}
if (r % 2 == 0) {
RightProd = ope(X[r], RightProd);
r--;
}
l /= 2;
r /= 2;
}
return ope(LeftProd, RightProd);
}
}
F - Connection Lights
$N \times M$の長方形グリッドがあり、各グリッドに$0$または$1$を割り当てることができます。 条件を満たす割り当て方を数え上げる問題です。
問題文が結構複雑で難しいですが、条件は次のような感じです。
すべての列に対して11、つまり「今見ている列とその隣の列が1」となるような行が$K$個以上存在する
というものです。
00 01 10 11 11
という割り当ては$K \leq 2$であれば条件を満たします。なぜなら、1列目4行目と1列目5行目に11があるからです。
$M$列の割り当てに対しては、$M - 1$列目まで同様の判定をします。
さて、「各列が条件を満たすかどうか」は隣の列に対して影響を及ぼすため、独立ではありません。 数学でどうにかするのがしんどそうな感じです。 この時点で割とdp濃厚になります。
そこで、前の列から順番に割り当てを決めていくことにしましょう。 最新列が条件を満たすためには、一つ前の割り当てさえわかれば十分です。さらに、それより前の列に対しては、条件を満たしさえすればどのような割り当てでもOKです。
以上より、全体の問題を小問題に分解できます。 $\mathrm{dp}[i][j] \coloneqq \text{先頭$i$列の割り当てをして、$i$列目の割り当て状況が$j$である場合の数}$とすることで、うまく数え上げができます。
import std;
void main () {
int N, M, K; readln.read(N, M, K);
solve(N, M, K);
}
void solve (int N, int M, int K) {
const long MOD = 998244353;
auto dp = new long[][](M + 1, 1 << N);
// dp[i][j] := 先頭i列が条件を満たし、最新列のランプがjである場合の数
foreach (j; 0..(1 << N)) {
dp[1][j] = 1;
}
foreach (i; 1..M) {
foreach (j; 0..(1 << N)) {
foreach (k; 0..(1 << N)) {
int count = 0;
foreach (l; 0..N) if (0 < (j & (1 << l)) && 0 < (k & (1 << l))) count++;
if (K <= count) {
dp[i + 1][k] += dp[i][j];
dp[i + 1][k] %= MOD;
}
}
}
}
long ans = 0;
foreach (i; 0..(1 << N)) {
ans += dp[M][i];
ans %= MOD;
}
writeln(ans);
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
この実装では$j$を2進数と解釈したときの「立っているbit」と1になっているグリッドを対応付けています。
このような手法をbit dpと呼ぶことがあります。
G - Play more!
$u _ 0 = 1, u _ k = N$であって、辺$(u _ i, u _ {i + 1})$に辺が存在する頂点列$(u _ 0, u _ 1, \dots , u _ k)$を考えます。 ある頂点の攻略に必要な時間を$a(u)$、ある辺を通行するのに必要な時間を$c(u, v)$と表記するとき、 この頂点列の満足度は$\sum a(u _ i) - \sum c(u _ i, u _ {i + 1})$と表現できます。
この値を最大化しましょう。これは、辺$(u _ i, u _ {i + 1})$に重み$a(u _ i) - c(u _ i, u _ {i + 1})$の辺をはったときの最長経路問題にすればよいです。 しかし最長経路問題を扱うのは面倒なので、どうにか既知の簡単な問題に直したいです。
そこで、辺の重みを反転して、$c(u _ i, u _ {i + 1}) - a(u _ i)$の辺を考えます。こうすることで、頂点$1$を始点とした最短経路問題に帰着します。 これによりはられた辺のコストは負になりうるので、ベルマンフォード法で処理します。
さて、infの処理をしましょう。ベルマンフォード法は(自分は理解していませんが)負閉路の検出ができるらしいです。
頂点$1$または$N$の強連結成分に負閉路が含まれているとき、なんかいい感じに伝搬させることができます。
この辺りは別途勉強して、(余裕があれば)エントリにします。
import std;
void main () {
int N, M; readln.read(N, M);
auto A = readln.split.to!(int[]);
// 辺の重みをc - Aにすると最短経路問題に帰着
solve(N, M, A);
}
void solve (int N, int M, int[] A) {
auto graph = new Tuple!(int, int)[][](N, 0);
foreach (i; 0..M) {
int a, b, c; readln.read(a, b, c);
a--, b--;
graph[a] ~= tuple(b, c - A[a]);
}
auto dist = new long[](N);
dist[] = long.max;
dist[0] = 0;
// bellman-ford
foreach (_; 0..N - 1) {
foreach (i; 0..N) {
if (dist[i] == long.max) continue;
foreach (to; graph[i]) {
int v = to[0];
long c = to[1];
if (dist[v] <= dist[i] + c) continue;
dist[v] = dist[i] + c;
}
}
}
foreach (_; 0..N - 1) {
foreach (i; 0..N) {
if (dist[i] == long.max) continue;
foreach (to; graph[i]) {
int v = to[0];
long c = to[1];
if (dist[i] == -long.max) {
dist[v] = -long.max;
continue;
}
if (dist[v] <= dist[i] + c) continue;
dist[v] = -long.max;
}
}
}
if (dist[N - 1] == -long.max) {
writeln("inf");
}
else {
writeln(-dist[N - 1] + A[N - 1]);
}
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
H - Just Solitaire
全く解けず…
単純な貪欲は無理そうです。 dpを考えようとしても、あるボーナスを受け取るためにはこれまでのカードの使用状況を記録しなければならないため、$O(2^N)$程度の状態があり得ます。 現状の知識では太刀打ちできませんでした。
問題に対する感想
全体を通して難易度調整がいい感じだと思いました。 典型パンチで倒せる問題がいくつかあり、想定レベルの参加者(私くらい?)にとって良い練習になったのではないかと思います。
懇親会も出ました。
オンサイトコンテストで他人と会話した経験がほとんどなかったのですが、本コンテストにおいては近くの方とお話しすることができました。
私は、私のことを他人から言及されているのを見てニヤニヤするタイプなので、他の人もそうだろうと仮定していくつか書きます。 あまり校正していない(する気がない)ので、乱文注意です。
まず、コンテスト開始前から終了後までcoindarwさんとお話することができました。 開始前はやることがなくてずっと席に座っていたのですが、声をかけてもらえてうれしかったです。 coindarwさんとはc++や競技プログラミングに関する話題で(自分的には)盛り上がった気がします。 ボス問が燃やす埋めるで解けるというのも教えてもらいました(理解はできていません)。このあたりのアルゴリズムは全く理解していなかったので、青コーダーはさすがだなぁと思いました。
横の席に西村さんが座っていたので、少しだけコンテストに関してお話しました。西村さんはRealforceを持ち込んで使用しており、業プロerだ…と思いました。(持たせてもらいましたが、だいぶ重たかったです。フルサイズだしそれはそうか。) ベルマンフォードを検索で通したというのを褒めてもらって、ちょっと嬉しかったです。 私、実はMMA015の時にもCを検索で強引に通したりしています。謎のゴリ押し得意なのでしょうか。 西村さんは私のTwitterアカウントを開設してから初めてフォローしてくれた競技プログラミング界隈の方なので、印象に残っていました。(当時、界隈の方を誰もフォローしていなかったはずなのですが、どうやって見つけたんでしょうか)
それから真鍋愛さんという方が加わり、ゲームやアニメの話などをしました。当日私は ハヤトの野望 というyoutuberのファングッズを身に着けていたのですが、真鍋さんもハヤトの野望のファンらしく、リアルでハヤトの話ができて楽しかったです。 フロムゲーに関する話題もありました。自分は名前しか知らなかったのですが、機会があればプレイしてみたいです。(地底人とかいう謎の単語が印象に残っています。) それと、coindarwさんとまぞくについての話をもっとしたかったなぁという若干の心残りがあります。(← それよりも、早く感想エントリを書かなければ)
それからやきとりさん、sepaさん、くしらさんが加わり、人数多めでお話ししました。 このあたりで気が付いたのですが、私のハンドルネーム「InTheBloom」、呼ばれるととても恥ずかしいです。こんなヤバ目のハンドルネーム、そうそういない気がします。今更ですが、割と後悔していたり。でも気に入っているんですよね。 元は「In」というのがあり、そこに「TheBloom」を付け足した形がこれなので、全部Inで統一しようかと真面目に考えてます。
若干話がそれました。 そこからはやきとりさん、sepaさん、くしらさんたちがMMAについての話などをしているのを聞いていました。緑以下第三回やMMA019オンサイトの可能性が示唆されており、楽しみだなーと思って聞いていました。 そこからは大体競技プログラミング関連のお話をしていました。二分探索のlogとsetのlogの重さが全然違う話など、だれに通じるんだよみたいな話が飛び交っており、面白かったです。 どなたかがatkinの篩を持っているという話をしていたのが印象的です。(何に使うんだろう)
社交が苦手な私ですが、競技プログラミング界隈の方とお話しするという貴重な経験をすることができました。 特に、電通大競技プログラミングコミュニティでお世話になっているcoindarwさん、やきとりさん、sepaさんとお話できてよかったです。
終わりに
オンサイトで、かつ難易度がちょうどいいものには積極的に出ようと思っています。 次回も楽しみです。