ナップサック問題の復元

はじめに

今回は ABC441F - Must Buy を題材にして、ナップサック問題の最適解を与える操作列を復元する手法を解説します。

ナップサック問題の解法

ナップサック問題とは、次の問題のことです。

容量が$M$のナップサックと、$N$個の物がある。 $i$番目の物は価値が$V[i]$、大きさが$P[i]$である。 ナップサックに入れる物を$0$個以上選び、容量制限を守りつつ価値を最大化せよ。

これを解くためには、次のような部分問題を設定します。 $$\mathrm{dp}[i][j] \coloneqq 先頭i個のものそれぞれを高々1つとり、重さがjであるとき実現できる最大価値$$ この部分問題を$i$の昇順に更新します。 $i = j = 0$は物をどれも選んでいない状態に該当すると考えて、$\mathrm{dp}[0][0] = 0$としておきます。 $i = 0, 0 < j$は実現不可能な状態なので、$\mathrm{dp}[0][j] = -\infty$としておきます。 また、$0 < i$の部分問題は未定なので、暫定的に$-\infty$としておきます。

更新はある状態から物をナップサックに入れるか入れないかの2通りで、入れない場合を $$\mathrm{dp}[i + 1][j] = \max(\mathrm{dp}[i + 1][j], \mathrm{dp}[i][j])$$ として、入れる場合を $$\mathrm{dp}[i + 1][j + P[i]] = \max(\mathrm{dp}[i + 1][j + P[i]], \mathrm{dp}[i][j] + V[i])$$ として表現します。

これらを行った後、$\max _ {0 \leq j \leq M}(\mathrm{dp}[N][j])$がありえる最大価値になります。

復元

ABC441Fで求められている通り、各物に対して、

1. その物を入れないで最大価値を達成することができない
2. その物を入れて最大価値を達成することができない
3. どちらでもない

のいずれであるかを判定することを目標にします。 これらの判定は、動的計画法の部分問題を頂点、遷移を辺と見て可視化すると理解しやすくなります。

下図はサンプル1に対する初期のdpテーブルを示した図です。 はじめ、$\mathrm{dp}[0][0]$だけ埋まっていて、残りは$-\infty$です。 赤矢印はdpの遷移を表しており、右にまっすぐ進む遷移は物1をナップサックに入れないこと、右下に進む遷移は物1をナップサックに入れることに対応しています。

下図はすべての部分問題を解いた後のテーブルの様子です。 各マスにはその条件で達成できる価値の最大値を記録してあります。 残った矢印は「実際にmaxを更新できた遷移」です。 （例えば、テーブルにおいて$\mathrm{dp}[i][j] < \mathrm{dp}[i + 1][j]$となっている部分は右矢印がありません。これはその遷移によって最大値を取らなかったためです。）

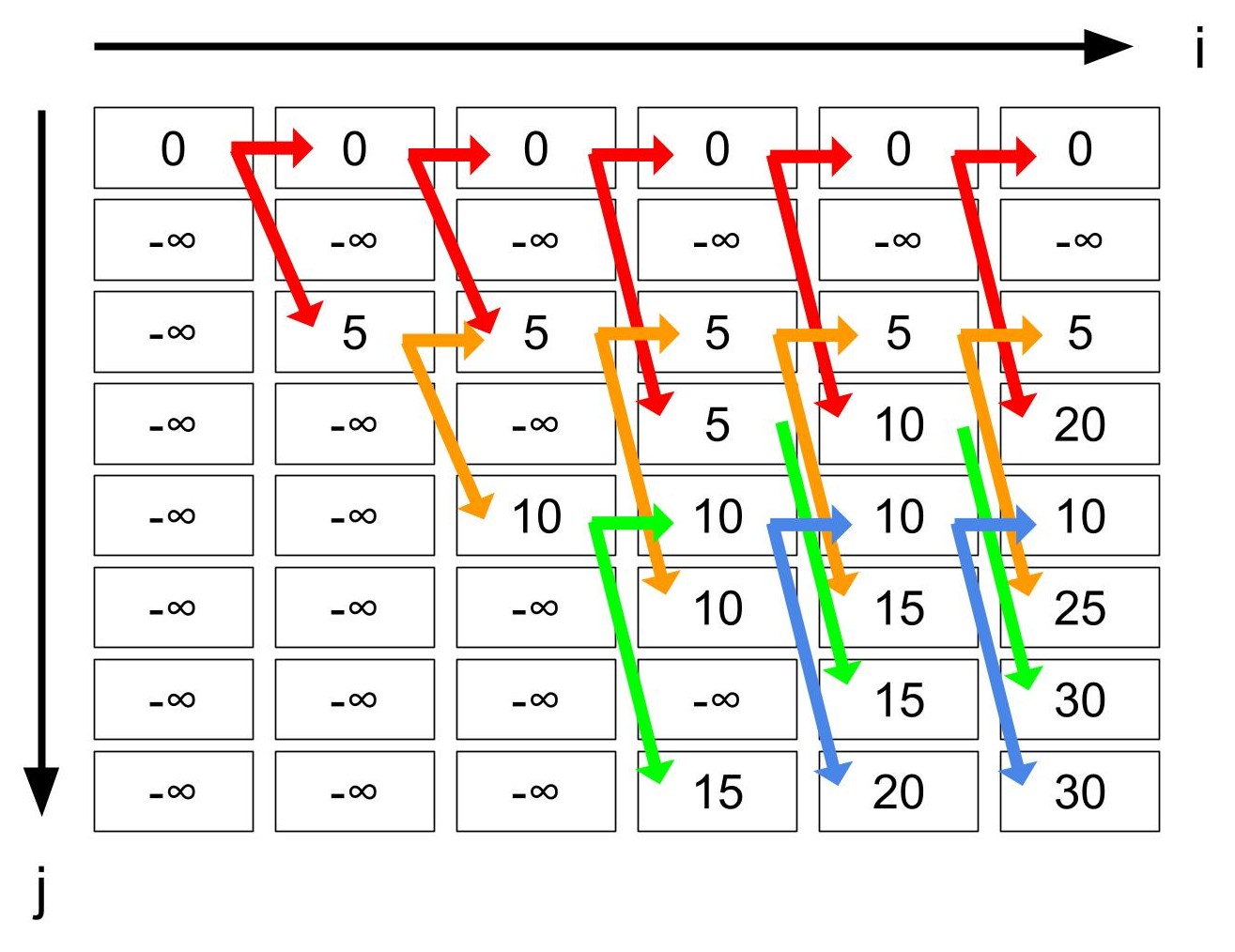
復元は$i$の降順に考えます。 例えば$\mathrm{dp}[5][7]$と$\mathrm{dp}[5][6]$は$30$であり、このナップサック問題に対する最大価値となります。 次に、矢印を1回たどってそれらのマスにたどり着けるマスを考えてみましょう。 以下の図の赤いマスが最大価値を与えるマスで、緑のマスが有効な遷移で赤いマスにたどり着けるマスです。

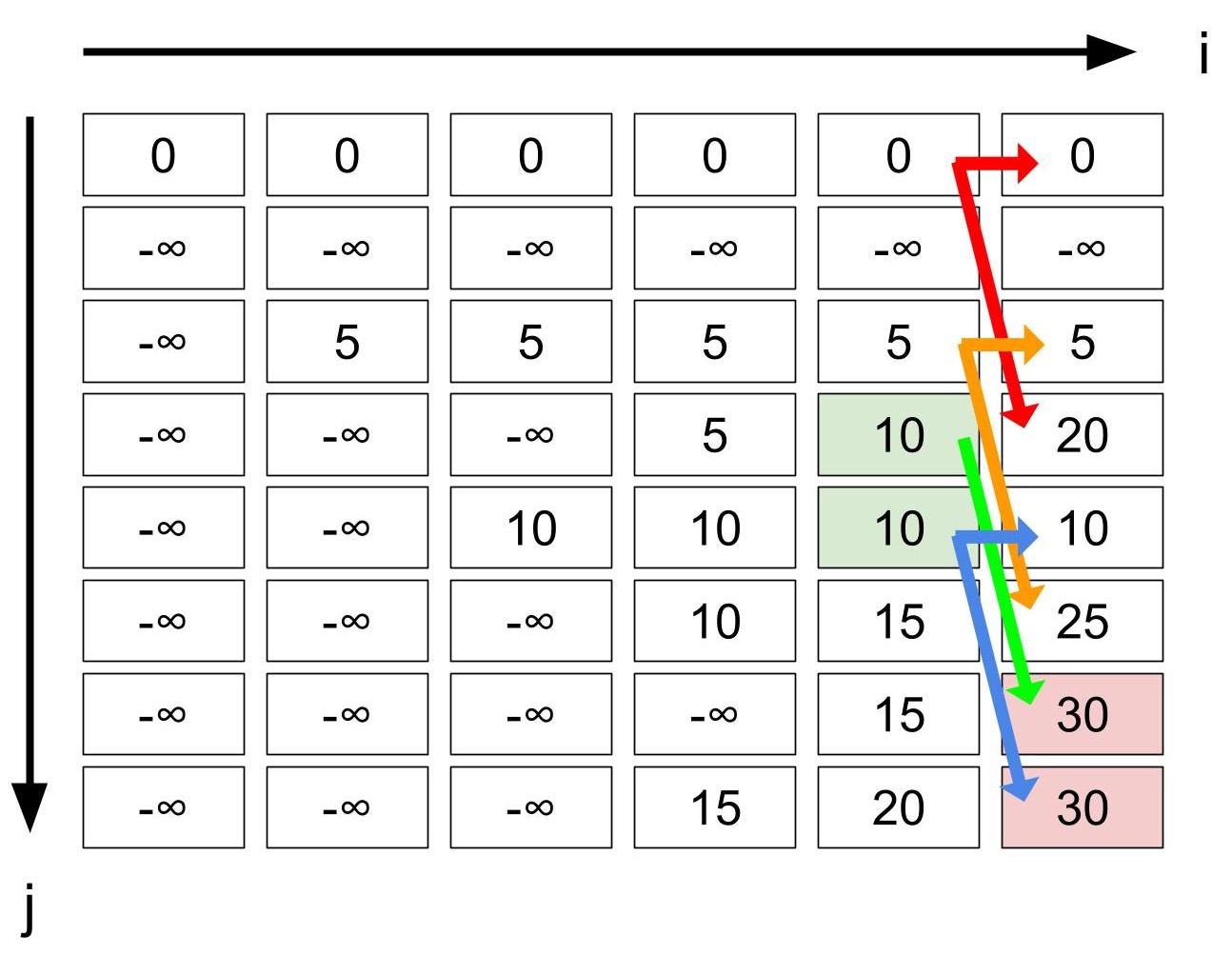
赤いマス、緑のマス、矢印の関係を考えてみます。 まず、各マスは「先頭$i$個のものそれぞれ高々1つとり、重さが$j$であるときに実現できる最大価値」を、矢印は、物をナップサックに入れるかどうかの選択を表すのでした。 ということは、赤いマスに矢印が伸びていないマス（緑のマス以外）はこの時点で 「最後の物を取ろうが取らまいが、最適解にはなりえない状態」 であることがわかります。

また、緑のマスから右下に伸びる矢印以外で赤マスにたどり着けないことから、このナップサック問題のインスタンスでは 「最後のものを取らないという選択をした場合、最適解になりえない」 ということもわかります。 以上より、最後の物は、最適解にたどり着くためには必ず入れる必要があることがわかります。

さて、それ以前の物について考えてみましょう。 とはいっても考え方は同じで、最終的に赤いマスに続くパスが存在するマス以外は最適解になりえないので、今度は緑のマスが目的地になります。 下図は後ろから2番目の物による遷移のみ残した図です。 緑のマスに行けるマス（黄色のマス）のみが最適解になりえる状態であり、さらに、物を取る遷移と取らない遷移両方が存在します。 つまり、この物を取る最適解と取らない最適解が両方存在します。

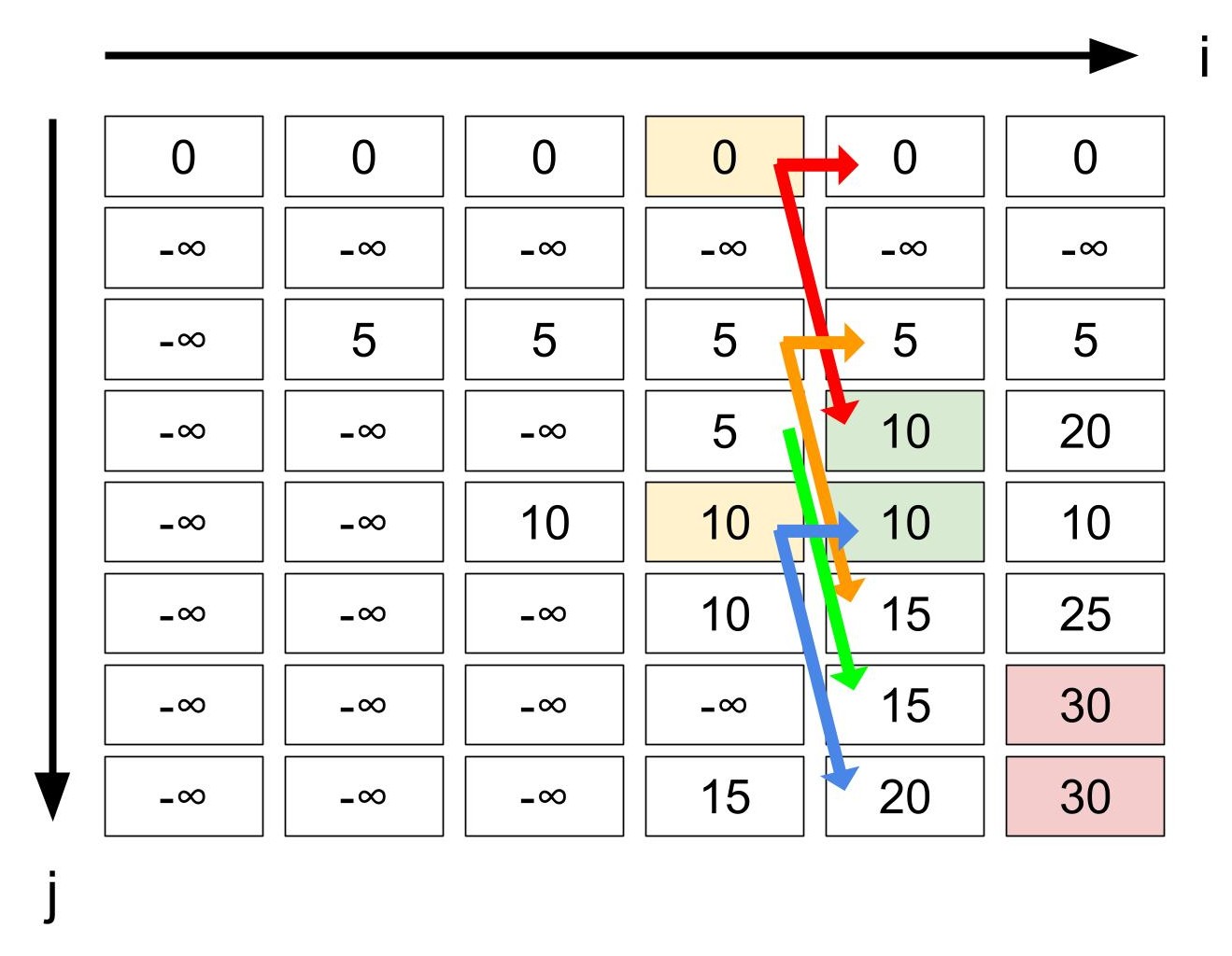
結局、この問題は「dpにおいて、状態と遷移の有向グラフを考えたとき、いくつかの頂点に対して使える辺を制限してもゴールへのパスが存在するか」を問うものだと言えそうです。 例えばこのグラフにさらに一工夫加えて、「最大価値かつ入れた物の数が最大である選び方を1通り示す」等もできそうです。（DAGの最長経路問題に帰着。）

実装例

ABC441F - Must Buyに正解するプログラムを掲載します。

提出（547ms/397340KiB）

import std;

void main () {
    int N, M;
    readln.read(N, M);
    auto P = new int[](N);
    auto V = new int[](N);
    foreach (i; 0 .. N) {
        readln.read(P[i], V[i]);
    }

    auto dp = new long[][](N + 1, M + 1);
    foreach (i; 0 .. N + 1) {
        dp[i][] = -long.max;
    }
    dp[0][0] = 0;

    foreach (i; 0 .. N) {
        foreach (j; 0 .. M + 1) {
            if (dp[i][j] == -long.max) {
                continue;
            }

            // 取らない
            dp[i + 1][j] = max(dp[i + 1][j], dp[i][j]);
            // 取る
            if (j + P[i] <= M) {
                dp[i + 1][j + P[i]] = max(dp[i + 1][j + P[i]], dp[i][j] + V[i]);
            }
        }
    }

    // 最大価値
    long mVal = 0;
    foreach (i; 0 .. M + 1) {
        mVal = max(mVal, dp[N][i]);
    }

    // 二次元グリッドにおいて、
    // 1. (i, j) -> (i + 1, j)
    // 2. (i, j) -> (i + 1, j + P[i])
    // の2本の辺を貼ったグラフだと考える。
    // ただし、辺が効力を持つのは
    // 1. dp[i][j] = dp[i + 1][j]
    // 2. dp[i][j] + V[i] = dp[i + 1][j + P[i]]
    // が満たされるときのみとする。
    // まず、(N, *)のうちmValを持つマスが最終到達目標。
    // (N - 1, *)のうち、そのようなマスに行ける場所を列挙する。
    // 1の辺が伸びている場合、そのアイテムを使わずとも目標地点に行ける。
    // 2の辺が伸びている場合、そのアイテムを使って目標地点に行ける。
    // 今度は目標地点へのパスが存在する頂点が新しい目標地点になっている。

    auto type = new int[](N);
    auto isGoal = new bool[](M + 1);
    auto nIsGoal = new bool[](M + 1);
    // 初期の到達目標
    foreach (i; 0 .. M + 1) {
        if (dp[N][i] == mVal) {
            isGoal[i] = true;
        }
    }

    foreach_reverse (i; 0 .. N) {
        nIsGoal[] = false;
        foreach (j; 0 .. M + 1) {
            if (dp[i][j] == -long.max) {
                continue;
            }

            if (isGoal[j] && dp[i][j] == dp[i + 1][j]) {
                nIsGoal[j] = true;
                type[i] |= 0b01;
            }
            if (j + P[i] <= M && isGoal[j + P[i]] && dp[i][j] + V[i] == dp[i + 1][j + P[i]]) {
                nIsGoal[j] = true;
                type[i] |= 0b10;
            }
        }
        swap(isGoal, nIsGoal);
    }

    auto ans = "";
    foreach (i; 0 .. N) {
        if (type[i] == 0b10) {
            ans ~= "A";
        }
        if (type[i] == 0b11) {
            ans ~= "B";
        }
        if (type[i] == 0b01) {
            ans ~= "C";
        }
    }

    writeln(ans);
}

void read (T...) (string S, ref T args) {
    import std.conv : to;
    import std.array : split;
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

別解

両側からdpすることもできます。 $$\mathrm{dp} _ 1[i][j] \coloneqq 先頭i個のものそれぞれを高々1つとり、重さがjであるとき実現できる最大価値$$ $$\mathrm{dp} _ 2[i][j] \coloneqq 末尾i個のものそれぞれを高々1つとり、重さがjであるとき実現できる最大価値$$ を計算し、さらに$\mathrm{dp} _ 2[i][j]$の方を$j$の昇順にchmaxすることで $$\mathrm{dp} _ 2[i][j] \coloneqq 末尾i個のものそれぞれを高々1つとり、重さがj以下であるとき実現できる最大価値$$ としておきます。

もの（$P[i], V[i]$）を判定するときは、$0 \leq j \leq M$に対して$\mathrm{dp} _ 1[i][j] + V[i] + \mathrm{dp} _ 2[N - i - 1][M - j - P[i]]$を計算し、いずれかが最大価値となるならば、そのものを選んで最大価値を実現する選び方が存在することがわかります。 選ばない方もやり方はほぼ同じです。

提出（902ms/789224KiB）

補足

今回はdpを埋め終わった後に辺が有効だったかどうかを逐次計算しましたが、場合によってはどちらの遷移が有効だったかを表す配列を用意したほうが良い場合があるかもしれません。 今回の問題では判定が簡単であること、空間計算量的に有利であることから逐次計算しました。