Functional GraphでK回進むクエリ in <O(NlogN), O(logN)>
Published on 2024-10-19Last Modified 2024-10-19
Table Of Contents
概要
次の問題を$\langle O(N\log N), O(\log N) \rangle$で解くアルゴリズムを紹介します。
問題
$N$頂点の有向グラフがあり、頂点$i$を始点とする辺の終点は頂点$f(i)$である。 次のクエリを$Q$個処理せよ。
- 頂点$u$から$K$回進んだ頂点を出力する。
$N \leq 2 \times 10^5$、$K \leq 10^{18}$
解法
Functional Graphにおいて、頂点を任意に一つ選んだとします。 この頂点はちょうどひとつのサイクルに含まれるか、あるいはどのサイクルにも含まれません。 すなわち、$i$を始点、$i$を終点とし、$i$をちょうど2個含むようなwalkはどの$i$に対しても一意、または存在しません。
理由
そのようなwalkを2通り以上とれたとします。これらwalkの中から任意に2つ取ります。 この2つで初めて異なる頂点が出現する場所を考えます。(このような場所は、最後が$i$であるという制約から必ず存在します。) この時、その場所の一つ前にある頂点の出次数が少なくとも2である事がわかりますが、これは仮定に反します。
この事実により、Functional Graphを互いに交わらないサイクルと、これらサイクルに「突き刺さっている」木に分解できます。 以下はFunctional Graphの例です。頂点7が「突き刺さっている木」で、他はサイクルです。
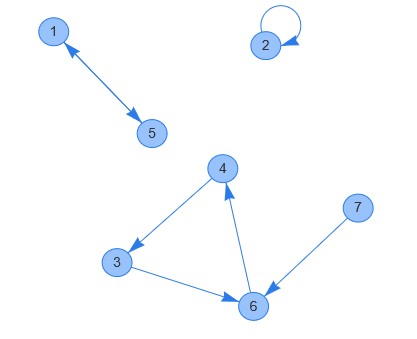
( https://hello-world-494ec.firebaseapp.com/ で作成)
事前にこれらのサイクルを列挙することが出来れば、サイクル内の点に対するクエリは$O(1)$で処理可能です。また、サイクル外の点は高々$N$回の移動で必ずサイクルに入るため、移動を行えばサイクル内の点に対するクエリに帰着できます。 移動先は一意なので、ダブリングで高速化することが出来ます。
このアルゴリズムの計算量を見積もります。 サイクルの列挙は$O(N)$時間で出来ます。ダブリングの前計算は$O(N\log N)$時間で出来ます。 クエリ処理は最悪ケースで$N$回の移動が必要で、これは前計算を用いて$O(\log N)$時間です。 したがって、$\langle O(N\log N), O(\log N) \rangle$です。
実装
next[i]を頂点$i$から1回進んだ先とします。
サイクル検出はいろいろやり方があると思います。次に示すコードはあくまで一例です。
auto vis = new bool[](N);
vis[] = false;
foreach (i; 0..N) {
if (vis[i]) continue;
work.length = 0;
int cur = i;
while (!vis[cur]) {
vis[cur] = true;
work ~= cur; // push_backです。
cur = next[cur];
}
foreach (idx, v; work) {
if (v == cur) {
// work[idx..]にサイクルが入っているので、なんやかんやする。
break;
}
}
}
ダブリングは次のような感じです。
// ダブリング構築: O(NlogN)時間
foreach (i; 0..N) {
doubling[0][i] = next[i];
}
foreach (i; 0..max_table_size - 1) {
foreach (j; 0..N) {
doubling[i + 1][j] = doubling[i][doubling[i][j]];
}
}
doubling[i][j]は$j$から$2^i$回進んだ先です。$2^i = 2^{i - 1} + 2^{i - 1}$である事を利用してテーブルを埋めます。
二次元配列は1次元目を指数、2次元目を頂点にした方が圧倒的に高速なので、これに従うほうが良いです。
max_table_sizeは$K$に依存せず、$O(\log N)$程度でよいことに注意してください。
これらを用いてクエリ処理します。ダブリングで進める時、msb側からほぐすと定数倍有利かもしれません。 通常のダブリングとは進め方が異なるので注意してください。 具体的には、$j$bit目が立っているかを見るのではなく、$2^j$進んで良いか(クエリで聞かれている分を超えないか)を見ます。
実装例
ABC367E - Permute K times (LDC 1.32.2 / 70ms)
import std;
void main () {
int N;
long K;
readln.read(N, K);
auto X = readln.split.to!(int[]);
auto A = readln.split.to!(int[]);
X[] -= 1;
auto fg = new FunctionalGraph(N);
foreach (i; 0..N) {
fg.add_edge(i, X[i]);
}
fg.build();
auto B = new int[](N);
foreach (i; 0..N) {
int j = fg.move_k(i, K);
B[i] = A[j];
}
foreach (i; 0..N) {
write(B[i], i == N - 1 ? '\n' : ' ');
}
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
class FunctionalGraph {
int N;
int[] next;
int[] roop;
int[] roop_start;
int[] roop_size;
int[] place;
int[][] doubling;
int max_table_size = 0;
bool built = false;
this (int N) {
this.N = N;
roop = new int[](N);
roop_start = new int[](N);
roop_start[] = -1;
roop_size = new int[](N);
roop_size[] = -1;
place = new int[](N);
place[] = -1;
next = new int[](N);
next[] = -1;
import core.bitop : bsr;
max_table_size = bsr(N) + 1;
doubling = new int[][](max_table_size, N);
}
void add_edge (int from, int to)
in {
assert(next[from] == -1);
assert(0 <= from && from < N);
assert(0 <= to && to < N);
}
do {
next[from] = to;
}
void build ()
in {
foreach (i; 0..N) assert(next[i] != -1);
}
do {
// ループを検出: O(N)時間
auto vis = new bool[](N);
auto work = new int[](N);
int latest = 0;
foreach (i; 0..N) {
if (vis[i]) continue;
work.length = 0;
int cur = i;
while (!vis[cur]) {
vis[cur] = true;
work ~= cur;
cur = next[cur];
}
int start = -1;
foreach (w; 0..work.length) {
if (work[w] == cur) {
start = w.to!int;
break;
}
}
if (start == -1) continue;
int rs = latest;
int wl = work.length.to!int;
foreach (w; work[start..$]) {
roop[latest] = w;
roop_start[w] = rs;
roop_size[w] = wl - start;
place[w] = latest - rs;
latest++;
}
}
// ダブリング構築: O(NlogN)時間
foreach (i; 0..N) {
doubling[0][i] = next[i];
}
foreach (i; 0..max_table_size - 1) {
foreach (j; 0..N) {
auto v = doubling[i][j];
doubling[i + 1][j] = doubling[i][v];
}
}
built = true;
}
int move_k (int fr, long K)
in {
assert(0 <= K);
assert(built);
}
do {
// ダブリングしながらループに入った時点でreturn
foreach_reverse (i; 0..max_table_size) {
if (roop_start[fr] != -1) {
break;
}
if ((1 << i) <= K) {
fr = doubling[i][fr];
K -= (1 << i);
}
}
if (K == 0) {
return fr;
}
int suc = (K + place[fr]) % roop_size[fr];
return roop[roop_start[fr] + suc];
}
}
追加情報
この問題は(自分の知っている限り)最良$\langle O(N), O(1) \rangle$で解けます。 本稿においてダブリングで処理した部分は結局
- 木が与えられる。$K$回遡った先の頂点を答えよ。
という問題がとければよいです。これはLevel Ancestor Problemという名前がついていて、調べるとたくさん解法が出てきます。 それらの一部にリンクしておきます。
本アルゴリズムは時間計算量、空間計算量の点でこれらのアルゴリズムに劣ります。 一方、LAを用いる場合、すべての木についてLAを構築する必要があり、実装がさらに大変になることが予想されます。 (LAを用いる場合でもサイクル処理するパートはさぼれないことに注意。)
終わりに
いくつか書きたいことがあるので書きます。
ダブリングするときに[bit][x]のレイアウトをmsb側から1次元に直すとキャッシュにのりやすくなる説ある?(msbで貪欲にとるアルゴのために逆順にしている)
— In (@UU9782wsEdANDhp) October 17, 2024
ほぐすときにアクセスする場所が連続するメモリの位置が小さい順番にアクセスできる気がする。要検証。
漠然とこんなことを考えて、いろいろ試行錯誤していました。 なかなかうまくいかないのでfastestあたりを見ていたら、LayCurseさんがクエリ$O(\log N)$で解いていることに気づきました。 そんなことできるのか?と考えていたら解けたので書くことにしました。多分998回くらい再発明されてますよねこれ。
ちなみにツイートの内容は今のところ「あまり早くならなさそう」という結論です。かなり残念。
それと、ダブリングは書き方次第で速度が大きく変わるようで、いろいろとテクニックがあるようです。
一番わかりやすいのは頂点を2次元目にするテクで、dp[i][x]をdp[x][i]にするだけで2倍くらい早くなります。
さらに、オフラインクエリで良いなら、
foreach (i; 0..N) {
int cur = i;
foreach (j; 0..BIT) {
if (0 < (K & (1L << i))) cur = dp[j][cur];
}
}
ではなく、
auto ans = iota(N).array;
foreach (i; 0..BIT) {
foreach (j; 0..N) {
if (0 < (K & (1L << i))) ans[j] = dp[i][ans[j]];
}
}
とした方が劇的に早くなるようです。ループアンローリングみたいな原理なのかなと思いつつなんでしょうこれ? ダブリング、奥が深いと思いました。あとこういう高速化って誰が教えてくれるんですかね?
オンラインかつクエリ$O(\log N)$でできるシンプルなアルゴリズムとして、今回の手法もそんなに悪くないのではないでしょうか? ただ、ライブラリ化してしまえば実装コスト0なので、LAで$\langle O(N), O(1) \rangle$をやる方も書いてみたいです。 現状、アドベントカレンダーのネタ候補の一つです。
色々見た感じ、オンラインでクエリ$O(\log K)$の方針を選ぶとどんなに頑張ってもdmdで400msくらいですが、このアルゴリズムなら200msを切れます。 そう考えると実用的かもしれないと思いました。(というか、今後Functional Graphのシミュレーションクエリが来たらこれ貼ります。)
ダブリングが重いのとてもわかります。
— In (@UU9782wsEdANDhp) February 29, 2024
始点一つに対して計算できればよいのであれば、こちらhttps://t.co/9uM3BWZoJI
が定数倍軽めかつ統一的に扱えるのでおすすめです。
実際、今年2月の私もダブリング重いよな~と思っていたようです。