[覚書] 陽なDAG上のdpを楽に処理する

定義

本稿におけるDAGとは、次のことを指します。

有向グラフ$G$であって、任意の$v \in V(G)$に対して次の条件を満たすもの。

• 始点と終点が$v$であり、かつ少なくとも一つの辺を通る経路が存在しない。

概要

AtCoderの過去問は、暗黙的なDAG上のdpが多い一方、明示的なDAG上のdpをする問題が少ないです。 そのため、明示的なDAGを渡されたとき、dpをすればよいということがわかっていたとしてもうまい実装が思い浮かばない方は多いかと思います。

私もそのような場面に何回か出くわし、そのせいで大幅にパフォーマンスを落とした経験があります。 そこで、それなりに汎用的であると思われるやり方を提案します。 なお、これは「灯台下暗し」的なもので、人によっては自明かと思います。

明示的なDAGのどこがしんどいのか

まずは、しんどくないdpについて考えましょう。 たとえば、よくある$$\mathrm{dp}\lbrack i \rbrack \lbrack j \rbrack \coloneqq (\text{$i$番目までを見たときに、…が$j$であるような…})$$といった形のdpは、 $$\mathrm{dp}\lbrack i + 1 \rbrack \lbrack j \rbrack = f(\mathrm{dp} \lbrack i \rbrack \lbrack k \rbrack)$$ といった形の計算により処理できることが多いです。この場合、単純なループ処理だけで計算ができます。更新順は、$i$を深さと見たときのbfs順ととらえることもできます。

さらに、木上のdpも非常に簡単に処理することができます。 これは木上の2点間のパスが一意に定まることが理由です。例えば、ある頂点から始めて配る遷移のdpをすることを考えます。 このとき、パスの一意性から1回目に出会った頂点の値を確定してしまってよいことがいえます。 つまり、普通にdfs巡回順で更新していくだけで正しい値が求まります。

これらのdpがbfsやdfs巡回順と同じ順番で出来るのは、ある程度単純なトポロジカル順序を持っているからと言えそうです。 では、一般のDAGではどうでしょうか。

結論から言うと、配る遷移をするとき、単純なdfsやbfs巡回順で更新すると値が壊れるようなケースが存在します。さらに、そのようなケースは極めて一般的です。

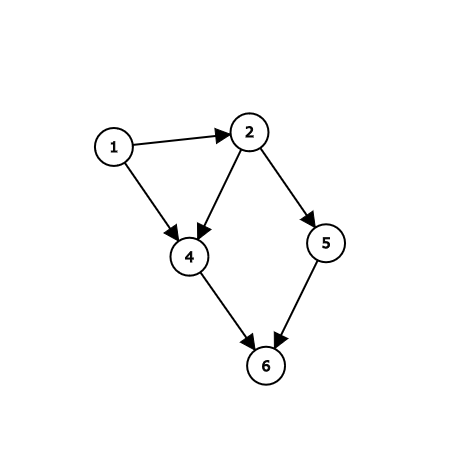
上の図はそのようなグラフの例です。例えば頂点4の値を正しく求めるには、頂点1と頂点2から配られた値が必要なはずです。 しかし、普通にbfsやdfsをすると、いつ頂点4の値が確定するかがわからないため、他の変数などを管理する必要が出てきます。 遷移以外に変数を管理する必要があるため、より面倒になりがちです。

一般のDAG上でのdpのしんどさについて説明したところで、次は処理方法の説明に入ります。

配るdp

頂点をトポロジカルソートをすると、dp部分をいつもの更新とほぼ同様に扱えます。 多くの場合は次の手順で解けると思います。

1. 頂点をトポロジカルソートする。
2. 頂点における答えを記録しておく配列に対して、スタート地点以外をすべて異常値で初期化しておく。
3. トポロジカルソートされた順番に頂点を見ていき、異常値なら無視、正常値なら遷移とする。

異常値を無視している理由は、一般のDAGの場合スタート地点の入次数が0とは限らないからです。スタート地点ではない場所からの遷移で値が壊れるのを防止しています。

ABC335Eに適用してみましょう。

この問題は、重みが等しい頂点をまとめて、重みが真に大きい方向にのみ辺を作ったDAGを考えると、最長経路問題に帰着します。 最長経路問題は配る遷移で解くことができるので、上記の方法を適用できます。

本稿で提案しているのはこの部分です。 いつものdpとほとんど同様に遷移できていることがわかると思います。

auto update_ord = topological_sort(graph);

foreach (v; update_ord) {
    if (dist[v] == -1) continue;
    foreach (to; graph[v]) {
        dist[to] = max(dist[to], dist[v] + 1);
    }
}

提出

もう一問例題を挙げておきます。 yukicoder No.2639を考えましょう。 こちらもグリッドグラフであることを除けばほぼ同じです。グリッドグラフからDAGを構築して、トポロジカルソートしましょう。

auto update_ord = topological_sort(graph);

vector<int> score(H * W, 1);
for (auto v: update_ord) {
    for (auto nex: graph[v]) {
        score[nex] = max(score[nex], score[v] + 1);
    }
}

提出

もらうdp

こちらの方が楽です。自分の子の値が確定してしまえばよいので、確定するまで再帰的に掘っていけば良いです。すなわち、メモ化再帰で実装するのが楽です。 この方法は意識せずに行っている方が多いかと思います。典型的な例でいうと、ゲームの後退解析などはこの例に当てはまります。 陽にグラフが与えられていたとしても、やることは同じです。

こちらも例題を提示しておきます。 ABC188Eを考えましょう。この問題は下流のDAGに属する頂点の最大の値が求まればよいです。 $\mathrm{dp}\lbrack i \rbrack \coloneqq (\text{頂点$i$より下流のDAGに属する頂点における最大の$A$})$とすると、子からもらう遷移になります。

具体的には、次のような遷移になります。

int[int] memo;
int dp (int pos) {
    if (pos in memo) return memo[pos];
    int res = -int.max;

    foreach (to; graph[pos]) {
        res = max(res, dp(to), A[to]);
    }

    return memo[pos] = res;
}

メモ化しないと計算が爆発するので注意です。

提出

終わりに

今週のUECCPでABC188Eを解きなおした際、mid_さんがこのメモ化再帰の解法について言及していたことがきっかけでこのエントリを作成しました。 今振り返ると、今までの自分はトポロジカルソートとdp更新を同時にやっていくようなあまり賢くない解法をとっていて、さらにそれが賢くないことに気づいてすらいなかったようです。

このエントリが、私の様に陽なDAG上でのdpに苦しむ人の助けになれば幸いです。