min_leftとmax_rightの仕組みと実装を理解する
Published on 2025-04-24Last Modified 2025-04-24
Table Of Contents
目的
AtCoder Library で使用できるatcoder/segtreeにおけるmin_leftおよびmax_rightが何を行っているかを理解し、自力で実装できるようになることを目指します。
min_left、max_rightとは
Segment Treeのことは一旦忘れて、いくつかの問題を考えてみましょう。
問題1
$N$個の商品があり、一列に並んでいます。左から$i$個目の商品は$A _ i$円です。(商品の値段は非負整数です。) あなたは$K$円持っていて、左から順番に商品を一つずつ買います。最大で何個の商品が買えますか?
購入した商品の合計額を保持しておけば$\Theta (N)$時間で解くことができます。
問題2
$N$個の商品があり、一列に並んでいます。左から$i$個目の商品は$A _ i$円です。(商品の値段は非負整数です。)次の$Q$個の質問に解答してください。
$x$個目の質問: あなたは$K _ x$円持っていて、左から順番に商品を一つずつ買います。最大で何個の商品が買えますか?
この問題は$\Theta (NQ)$時間より高速に解くことができます。(灰色くらいの難易度?) 商品の金額は非負であるため、一度総額が$K _ x$円を超えてしまうともう下回ることはありません。 この性質を利用して、解を二分探索で求めることができます。 $0 \leq i \leq N$に対して、左から$i$個買った時の金額はいくらか?を前計算しておくことで$\Theta (N + Q \log N)$時間で解くことができます。
さらに一般化した問題を考えます。
問題3
$N$個の商品があり、一列に並んでいます。左から$i$個目の商品は$A _ i$円です。(商品の値段は非負整数です。)次の$Q$個の指示に従ってください。指示はタイプ1とタイプ2の2種類があります。
タイプ1: $i, P$が与えられる。左から$i$個目の商品の値段を$P$円に変更する。
タイプ2: $K$が与えられる。左から順番に商品を一つずつ買うとき、最大で何個の商品が買えるかを出力。
タイプ2の指示を同じく二分探索で解くことにしましょう。問題2と同様に解こうとすると左から$i$個買った時の金額を知りたくなりますが、商品の値段が途中で変更されてしまうため、累積和を利用することができません。 代わりに和を計算するSegment Treeを利用することで問題を解決しましょう。
Segment Treeでは区間和の取得に$\Theta (\log N)$時間かかるため、全体では$\Theta (N + Q \log ^ 2 N)$時間で解くことができます。
より深掘りしてみましょう。 結局、問題3でやりたいことは、$A _ 1 + A _ 2 + \dots + A _ x \leq K$かつ$K < A _ 1 + A _ 2 + \dots + A _ x + A _ {x + 1}$を満たす$x$を見つけることと言えます。 これは、左端を固定して右端を伸ばしていくとき
- いずれ区間の値が特定の条件を満たさなくなる
- 一度条件を満たさなくなると、以後再度条件を満たすことはない
という2つの仮定をした上で、条件を満たす右端の限界位置を探すことだと解釈できます。 (今回でいうと、満たすべき条件は総和が$K$以下になること。商品の値段は非負整数なので一度超えるともう下回らない。)
実は、Segment Treeの内部構造を利用することで、このような$x$を$O(\log N)$時間で探し出すことができます。 min_leftやmax_rightはこの$x$を探すための関数なのです。
max_rightをもう少し抽象化しておきましょう。モノイド$(M, +, e)$、各要素が集合$M$に属する長さ$N$の数列$A = (A _ 1, A _ 2, \dots, A _ N)、$関数$f: M \rightarrow \lbrace 0, 1 \rbrace$(集合$M$の元を受け取って$0$か$1$を返す関数)が与えられたとします。
左端を固定したとき、ある右端までは条件をみたし、それ以降条件を満たさなくなるような状況を仮定します。つまり、 $1 \leq l \leq N$をひとつ固定したとき、全ての$l \leq x \leq N - 1$に対して$f(\sum _ {i = l} ^ x A _ i) \leq f(\sum _ {i = l} ^ {x + 1} A _ i)$が成立する状況を考えます。(この定式化では$\text{true}$に相当する値を$0$、$\text{false}$に相当する値を$1$としていることに注意。)
このとき、
- $f(\sum _ {i = l} ^ x A _ i) = 0$
- $x = N$または$f(\sum _ {i = l} ^ {x + 1} A _ i) = 1$
を両方満たすような$x$を探すアルゴリズムです。 min_leftもほぼ同様で、右端を固定した際に条件を満たす左端の限界位置を探します。
$f(\sum _ {i = l} ^ l A _ i) = 1$となる場合をどうするかは設計によります。 例えば、AtCoder Libraryでは$f(e) = \text{true}$(単位元が条件を満たすこと)を$f$に要請することで問題を回避しています。
仕組み
「どうやってアルゴリズムを発見したか」ではなく、「どういった仕組みで動いているか」を理解することに重点を置きます。 以降やや天下り気味にアイデアを見ていきます。
$l = 1$のケース
まずは$l = 1$のときを考えます。 $l = 1$を考えるのは、「左端が$l$であって、$r + 1$を含むセグメント(以後、各頂点をセグメントと呼びます。)」を容易に得られるからです。具体的には、最上階にあるセグメントはそのようなものの一つになっています。
簡単のため、上の章で紹介したものと同じ問題をさらに単純化して扱います。$N = 16$で全ての要素が$1$であるとします。 ある閾値$K$が与えられるので、区間和$\sum _ {i = l} ^ r A _ i$が$K$以下になる最大の$r$を探します。つまり、以下のような状況です。
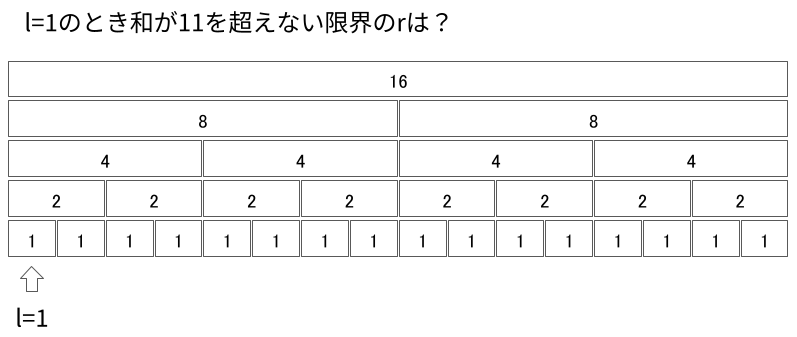
まず、「左端が$l$であって、$r + 1$を含むセグメント」を見つけます。この単純化されたケースではルートセグメントをとればよいです。
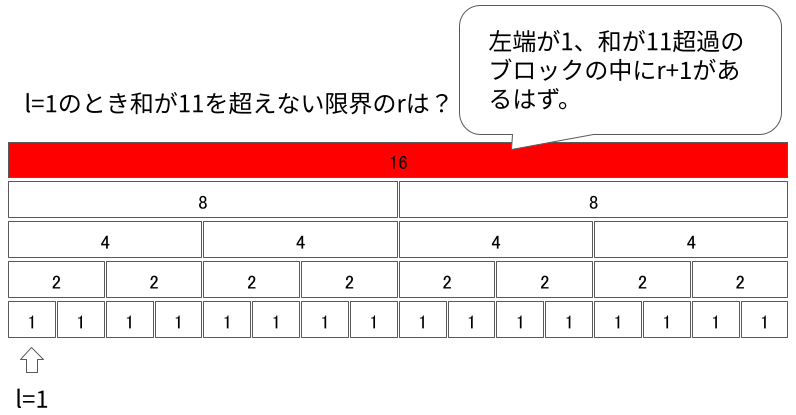
そのセグメントが子を2つもっている場合、$r + 1$がどちらに含まれるかを判定します。 単調性を仮定しているため、左のセグメントを含んだ時点で総和が$K$を超えていれば左に、そうでなければ右に含まれるとしてよいです。
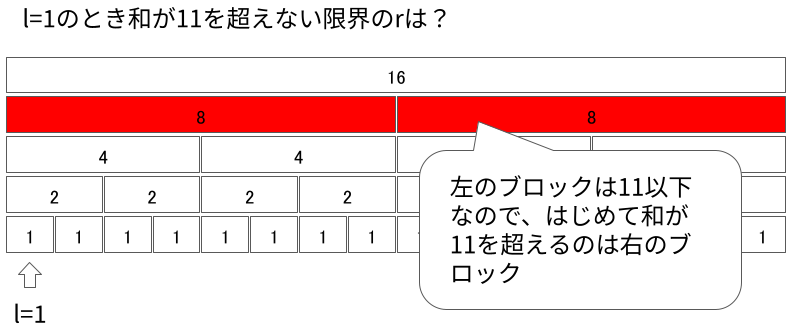
同様にしてSegment Treeを「降りて」行きます。
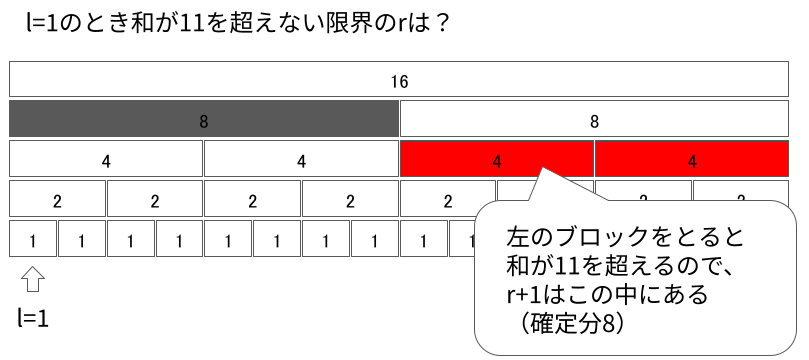
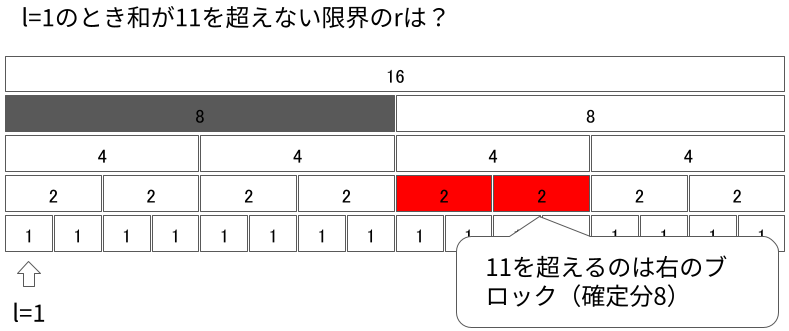
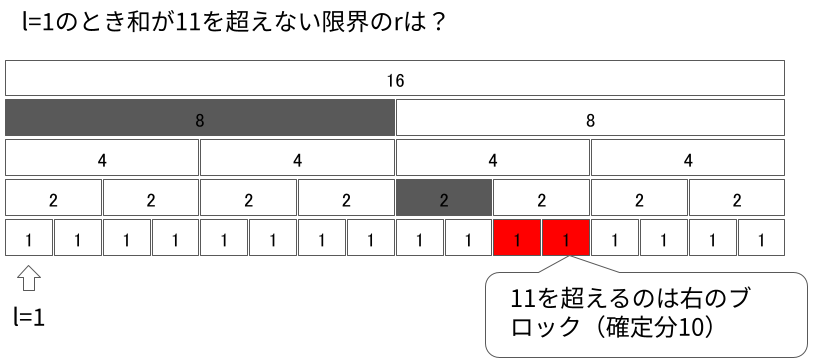
今見ているセグメントが最下層まで来たとき終了です。今見ているセグメントまで足すと条件を満たさなくなるという不変条件を維持していたため、求める$r$はそのひとつ左です。

このように、「左端が$l$であって、$r + 1$を含むセグメント」さえ見つかれば、$r + 1$が子のどちらに含まれているのかを考えながら降りていくことで見つけることができます。これらの工程はSegment Treeの高さに比例する時間がかかるため、$O(\log N)$時間で行うことができます。
任意の$l$に対するケース
次に、任意の$l$に対して考えてみます。 今度は逆に、下から適切に登っていくことで$l = 1$のような状況に帰着させます。 例として、$l = 4$の例を見ていきます。
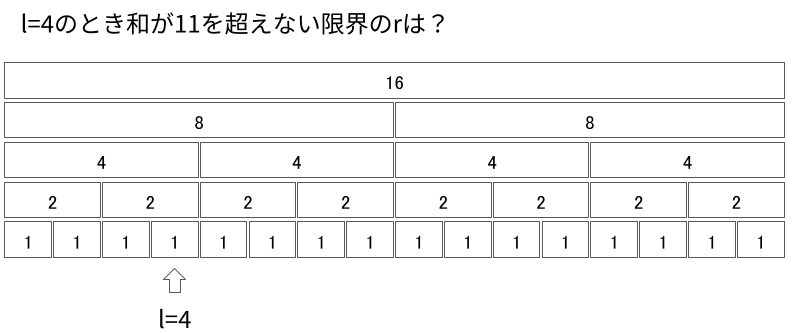
今見ているセグメントに$r + 1$が含まれるかを判定します。もし含まれない場合、より大きなセグメントに移動します。
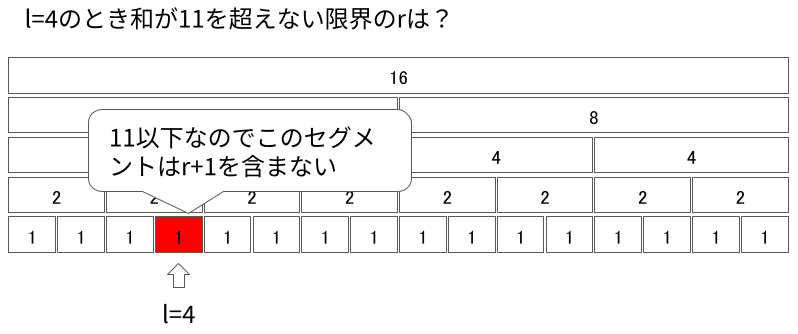
ただし、$l$より左にある要素を含むようなセグメントに行ってはいけません。真上に登れない(自身が右セグメントである)場合、そのセグメントは切り離して右に登ります。
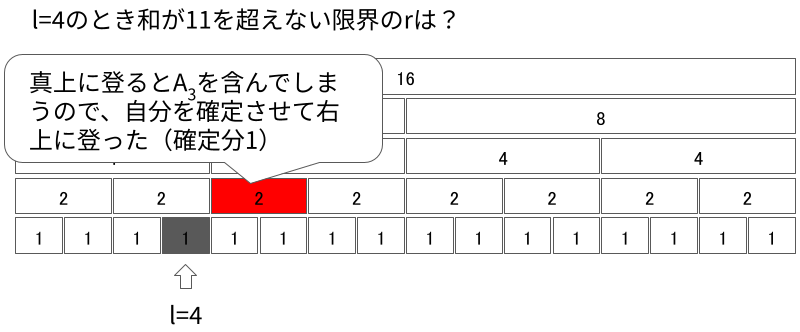
同様にして$r + 1$を含むセグメントになるまで登っていきます。
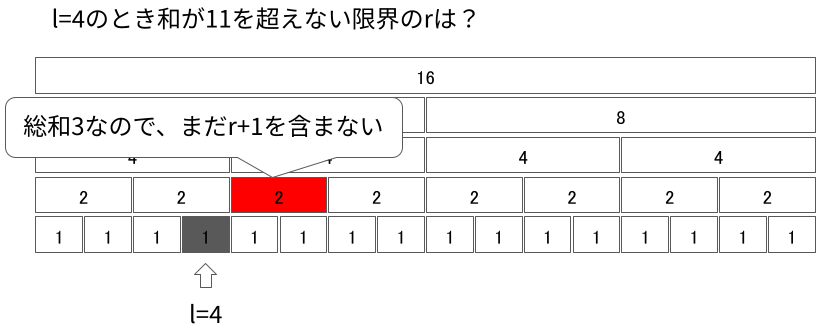
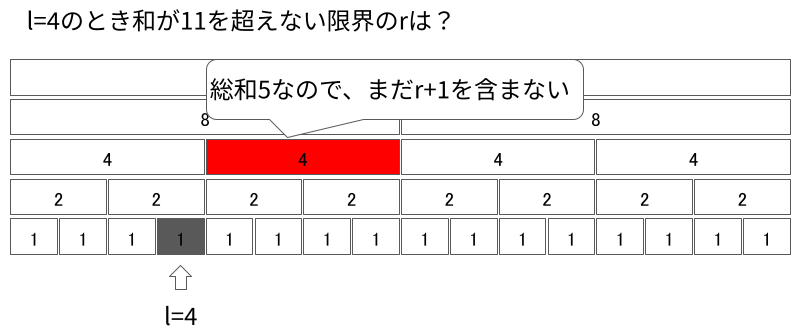

今見ているセグメントを含めて総和が11を超えれば、そのセグメントに$r + 1$が入っているということになります。

$r + 1$が入っているセグメントが見つかったら$l = 1$のケースに帰着できます。 先ほどと同様に、「今見ているセグメントを含めると条件を満たさなくなる」を不変条件として降りていきます。
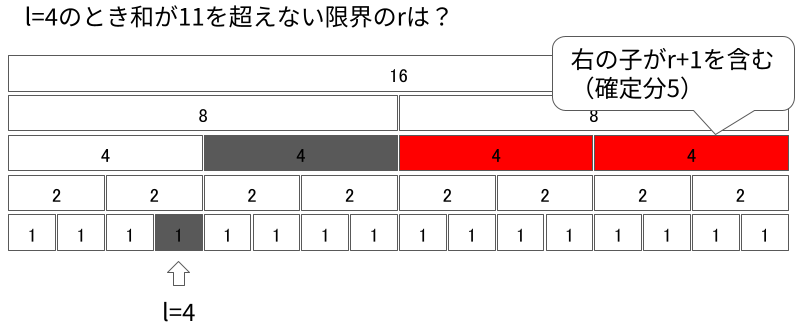
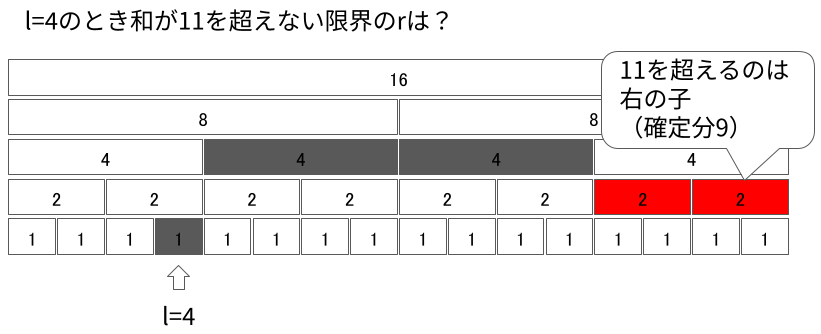
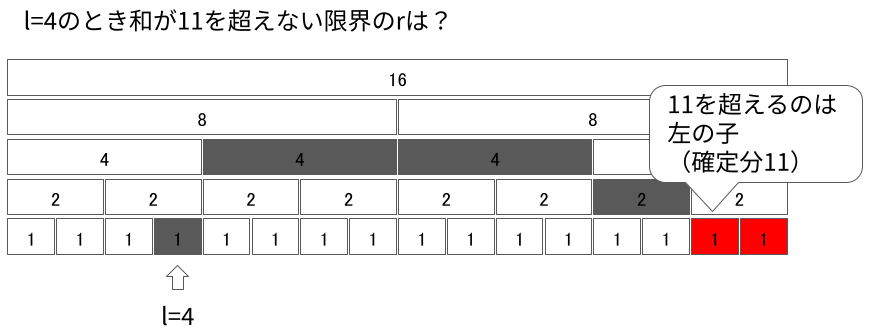
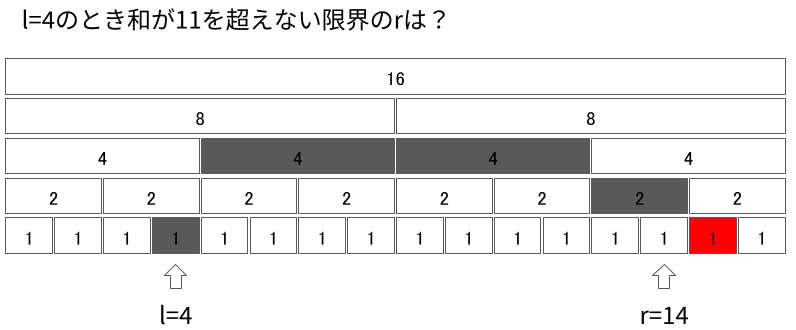
無事max_rightを求めることができました。
実装
以下にRange Sum Queryのみ対応したSegment TreeのC++実装例を示します。 しかし、Segment Treeの細部は人によって違いがあるでしょう。そのため、自分のSegment Treeで使いやすい形にアレンジするのをお勧めします。
私のSegment Treeに関して、留意すべき特徴を示しておきます。
- ルートセグメントが0番
- 2冪に合わせている
- 非再帰
- max_rightおよびmin_leftで判定関数にモノイドを渡したときtrueになることを要請せず、閉区間を基本にして扱う
コード全体の前に、max_rightの部分を解説します。解説はコード中のコメントに記載します。
template<typename F>
BinarySearchResult max_right (F f, int l) {
assert(0 <= l && l < length);
// コーナーケースを回避するために、
// 1. 右端まで全て含んでtrue
// 2. A[l]の時点でfalse
// となるケースをはじく。
if (f(prod(l, length))) {
return BinarySearchResult(length - 1);
}
if (!f(prod(l, l + 1))) {
return BinarySearchResult();
}
l += modified_length - 1;
T acc{};
// r + 1を含む区間が見つかるまで登る。
while (true) {
// 真上に登るとA[l]より左の要素を含むセグメントに行ってしまうため、
// 自分を確定させて右にずらす。
if (l % 2 == 0) {
acc += node[l];
l++;
}
// 登る。
l = (l - 1) / 2;
// r + 1を含む区間が見つかった。
if (!f(acc + node[l])) {
break;
}
}
// 今見ているセグメントが最下層にたどり着くまで降り続ける。
while (l < modified_length - 1) {
// どちらかのセグメントに進む。
if (f(acc + node[2 * l + 1])) {
acc += node[2 * l + 1];
l = 2 * l + 2;
}
else {
l = 2 * l + 1;
}
}
l -= modified_length - 1;
// 求めるrはたどり着いたセグメントのひとつ左にある。
return BinarySearchResult(l - 1);
}
コード全体を示します。少なくともC++20ならコンパイルできました。
#include <cassert>
#include <vector>
struct BinarySearchResult {
const bool empty_payload;
const int value_payload;
BinarySearchResult (): empty_payload(true), value_payload() {}
BinarySearchResult (int border): empty_payload(false), value_payload(border) {}
bool empty () {
return empty_payload;
}
int value () {
assert(!empty());
return value_payload;
}
};
template<typename T>
struct RSQSegmentTree {
int length{};
int modified_length{};
std::vector<T> node{};
RSQSegmentTree (int length_) {
assert(1 <= length_);
length = length_;
modified_length = 1;
while (modified_length < length) {
modified_length *= 2;
}
node.resize(2 * modified_length - 1);
}
T get (int i) {
assert(0 <= i && i < length);
return node[modified_length - 1 + i];
}
void set (int i, T value) {
assert(0 <= i && i < length);
int cur = modified_length - 1 + i;
node[cur] = value;
while (0 < cur) {
cur = (cur - 1) / 2;
node[cur] = node[2 * cur + 1] + node[2 * cur + 2];
}
}
T prod (int l, int r) {
assert(0 <= l && l < length);
assert(0 <= r && r <= length);
assert(l <= r);
if (l == r) {
return T{};
}
// 閉区間へ変換
l += modified_length - 1;
r += modified_length - 1 - 1;
T ret{};
while (l < r) {
if (l % 2 == 0) {
ret += node[l];
l++;
}
if (r % 2 == 1) {
ret += node[r];
r--;
}
l = (l - 1) / 2;
r = (r - 1) / 2;
}
if (l == r) {
ret += node[l];
}
return ret;
}
template<typename F>
BinarySearchResult max_right (F f, int l) {
assert(0 <= l && l < length);
if (f(prod(l, length))) {
return BinarySearchResult(length - 1);
}
if (!f(prod(l, l + 1))) {
return BinarySearchResult();
}
l += modified_length - 1;
T acc{};
while (true) {
if (l % 2 == 0) {
acc += node[l];
l++;
}
l = (l - 1) / 2;
if (!f(acc + node[l])) {
break;
}
}
while (l < modified_length - 1) {
if (f(acc + node[2 * l + 1])) {
acc += node[2 * l + 1];
l = 2 * l + 2;
}
else {
l = 2 * l + 1;
}
}
l -= modified_length - 1;
return BinarySearchResult(l - 1);
}
template<typename F>
BinarySearchResult min_left (F f, int r) {
assert(0 <= r && r < length);
if (f(prod(0, r + 1))) {
return BinarySearchResult(0);
}
if (!f(prod(r, r + 1))) {
return BinarySearchResult();
}
r += modified_length - 1;
T acc{};
while (true) {
if (r % 2 == 1) {
acc += node[r];
r--;
}
r = (r - 1) / 2;
if (!f(acc + node[r])) {
break;
}
}
while (r < modified_length - 1) {
if (f(acc + node[2 * r + 2])) {
acc += node[2 * r + 2];
r = 2 * r + 1;
}
else {
r = 2 * r + 2;
}
}
r -= modified_length - 1;
return BinarySearchResult(r + 1);
}
};
利用例
$(R _ q, C _ q)$から十字に伸ばしていったときに、最も近い1を探す問題です。
全てのマスに$1$がセットされた$H \times W$のグリッドをRange Sum QueryのできるSegment Treeで二つ持っておきます。 具体的には、
col[i]:=$i$行目の行を表すSegment Treerow[i]:=$i$列目の列を表すSegment Tree
とします。各クエリに対して、
col[R[q]]において$C _ q$からスタートして和が$0$である限界位置row[C[q]]において$R _ q$からスタートして和が$0$である限界位置
を+-方向で求められればよいです。 これはmax_rightとmin_leftが利用できます。
参考文献
インターフェースや実装方針を参考にしました。
本エントリの大部分はこの文献に基づいています。こちらも見に行くとよいかもしれません。 本エントリはこの文献の行間を埋める目的で書きました。
終わりに
max_rightおよびmin_leftは比較的定数倍の軽いアルゴリズムであるため、$O(\log N)$時間と$O(\log ^ 2 N)$時間の違いは結構効いてきます。 個人的になかなか美しいアルゴリズムだと思うので、是非実装してみてください。
今回のエントリではたくさんの画像を入れて読者が出来るだけ理解しやすいようにしたつもりです。 不明点、誤りなどがあれば教えてほしいです。試験的にgoogle formを設置してみました。もしよければ何か送信してみてください。(私が喜びます。)
注: 返信が欲しい場合は連絡先を含めてください。