精説ARC155A
Published on 2023-02-07Last Modified 2023-12-01
Table Of Contents
はじめに
先日1月29日に AtCoder Regular Contest 155 がありました。ARCのA問題は,ARCがA~Fの6問体制になったARC104から現在に至るまでdifficultyの最大値は緑でした。しかし,今回のA問題は水色でした。

現在レート400+程度の私にとって,ARCにおいては一問解くだけでパフォーマンス700+くらいが望めるので非常に「コスパのいい」大会だと思っていたのですが,今回のA問題が思いのほか難しく,一問も解くことができませんでした。
コンテスト後にもう少し粘ってみたら解けたので,(公式解説が思いのほかよくわからないこともあり)解法を残しておくことにします。
問題の概要
問題文は以下の通りです。

要約すると,「与えられた文字列をSとする。この時,Sの前にくっつけてもSの後ろにくっつけても回文になるような長さKの文字列が存在するか?」というものになります。
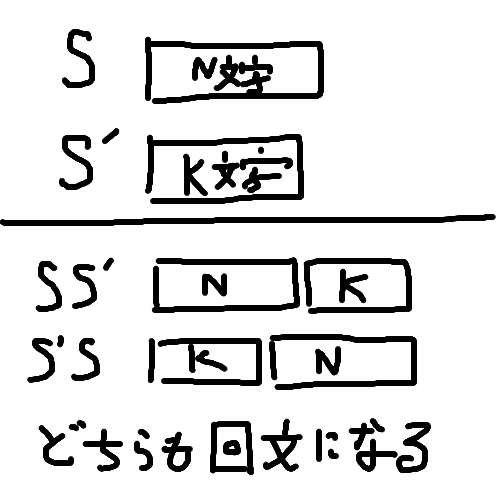
上の画像はビジュアル化したものになります。
方針
まず制約を見てみましょう。特筆すべき点は,Kがかなり大きくなる可能性があるということでしょうか。また,一つの入力に含まれるテストケースについて,Nの総和が2×10^5以下というのも重要そうです。一つの入力に与えられるテストケースの数が非常に多いからです。
さて,この問題を解くためにどうすればよいのでしょうか?数多くの方針があると思いますが,私はこういう時は最もシンプルな方針を試してみます。この問題に対して最もシンプルな方針は何でしょうか?それは与えられた条件からできるだけ実際にK文字のS'を構成するというものです。
幸い文字列Sは与えられるので,この考え方は試すことができそうです。
シンプルに考えてみる
さて,「実際に構成する」といったものの,どのようにすればいいのでしょうか?まずは以下の図をご覧ください。
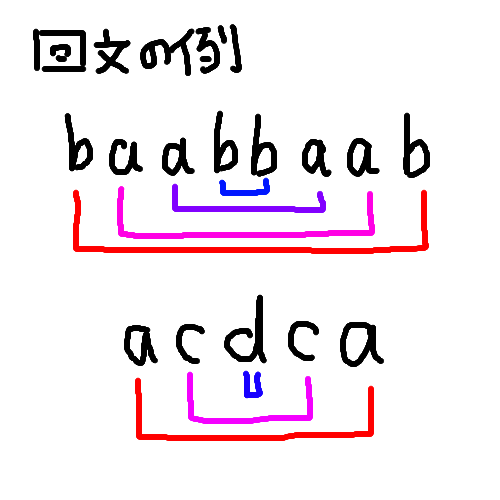
回文の定義を考えれば,「一番左にある文字」は「一番右にある文字」と同じで,それがずっと続くわけです。つまり,「左から〇番目にある文字」は「右から〇番目にある文字」と同じわけです。
すなわち,問題の題意を満たすような文字列S'が存在するなら,それは与えられた文字列Sの逆順の一部分に他ならないわけです。
さて,ここで一つ疑問がわきます。もし「与えられた文字列」が「構成しようとしている文字列」よりも長かった場合,今言った方法で構成しきることができます。しかし,もしそうでないなら?すなわち,構成しようとしている文字列が与えられた文字列よりも長い時に,残りの部分がどうなるのかを考える必要が出てきそうです。
K < N の場合
まずはややこしいパターンを考える前に,比較的簡単なパターンを処理してしまいましょう。
この時、前述のとおり各ケース実際にk文字分すべてを構成することができます。したがって、確認する必要があるのはS -> S'の順番で考えた時のS'と、S' -> Sの順番で考えた時のS'が一致するかどうかです。
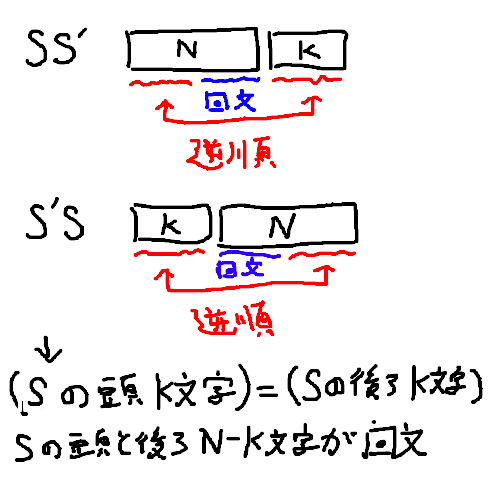
上にある画像の通り、回文となるようなS'が存在することを仮定すると、S'はどちらのケースでも同一であるという仮定から、
- 文字列Sの先頭K文字と末尾K文字が一致する
- 文字列Sの先頭N-K文字と、末尾のN-K文字が回文を成す
というSが要請される条件が見えてきます。このチェックにかかる計算量はO(N)になるので、制約的にも問題なさそうです。
K = N の場合
場合分けは漏らさずに考えることが必要です。イコールも忘れずにチェックします。先ほどのケースにこれを含めなかった理由は、場合分けはできるだけ細切れのほうが一ケース当たりに考えることが減るからです。
この時も同様に考えてみます。
- S S'が回文: S'はSの逆順そのもの
- S' Sが回文: S'はSの逆順そのもの
というわけで、Sに対してまったく条件が課されないことがわかります。単にS'をSの逆順として定めてしまえば任意のSに対して条件を満たすS'となります。この判定はO(1)なので当然オーケーです。
もしよくわからなかったら具体的に一ケース挙げて考えてみるといいと思います。(ex. S = "12345")
K > N 以降
小休憩
ここから少し複雑になります。そこで、今まで何のために場合分けをしていたのかを再確認しておきます。
ここまで、「最もシンプルな手」すなわち、「与えられた条件から実際にS'を構成してみて、そこから考える」という手段をとってきました。
ここで問題になるのは、「Kが非常に大きいケースにおいては、S'を構成するのに少し手間がかかりそう」という事実です。なぜKが小さいときにS'を構成しやすいかは ここ を見返してみてください。
よく見直してみると、K > Nのケースにもまだ比較的シンプルにS'を構成できるものが残っています。まずはそれを片づけましょう。
2N > K > N の場合
この時も、Sが与えられたらすぐにS'を構成することが可能です。なぜなら、以下の画像の通り、前からN文字、後ろからN文字が確定するのでS'が(存在するなら)一つに定まるからです。
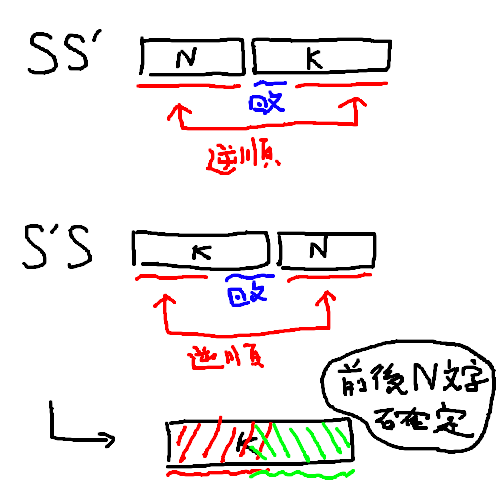
一見するとK > Nの場合と変わらないように見えますが、このケースにおいて回文の判定をするのはS'の中になるという違いがあります。従って、直接Sを評価して答えを出すことができるわけではなく、「S'が存在するなら、Sから構成したこの文字列は-な条件を満たす。」という説明付けになっています。最後はプログラムに落とし込まないといけないわけなので、やはりできるだけ分割は細かくしておくべきだとと思います。
この時、S'の満たすべき条件は以下の2つになります。
- S'の中心付近の(上図にも示されている)「重なり合う場所」で、互いに打ち消しあわない
- S'の先頭K-N文字と末尾K-N文字が回文を成す
前述のとおり、これは実際にS'を構成して確かめる必要があります。このチェックにはO(N+K)が必要ですが、十分間に合います。(計算量の見積もりあってるか自信ないです)
K = 2N の場合
今回も一応イコールを分けておきました。この時、S'を構成しても「互いに重なり合う場所」が発生しません。なので、条件は非常にシンプルになり、「Sが回文」が構成可能になる必要十分条件となります。
これも上の議論を考えれば直ちに従うので、もしわからなければ具体例を考えてみるといいかもしれません。(ex. S = "1234321", K = 14)
また、このケースは2N > Kのケースと全く同じ判定法を使うことができます。したがって、実際に実装するときは統合してもよいかもしれません。
K > 2N の場合
まず、これまでの議論から、S'が存在すると仮定すると次のことが言えます。「S'は先頭と末尾のN文字はSの逆順そのものである」「S'の先頭と末尾のK-N文字は回文を成す」
この情報から残りの部分がどうなる必要があるか考えます。
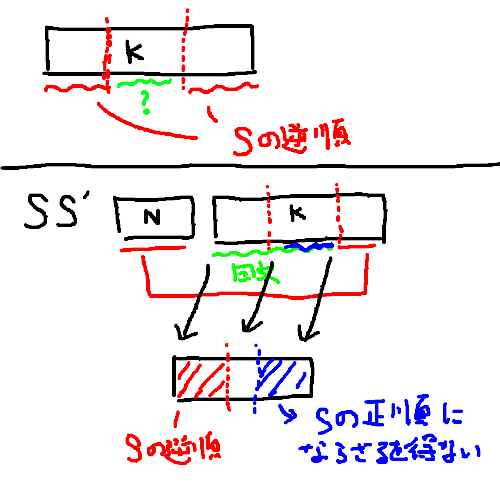
上に示した画像の通り、これらの情報からS'の不明だった場所が少しだけ確定させることができます。これと全く同じ議論をS' -> Sのパターンでも考えることによって、S'はSの逆順 > Sの正順 > Sの逆順 > ...という風に、2NずつSの逆順か正順のどちらかに挟まれていることがわかります。
これは、S'の残りの部分が2N未満になるまでまったく同様に続けることができます。結果的に、以下の図のようになります。
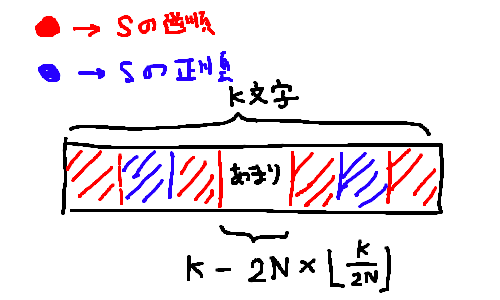
結局、この「あまり」の部分の周りについてのみ考えればよいことになります。この余りは0~2Nまでの値をとりますが,このあまりの部分の長さによって場合分けが発生することに注意する必要があります。
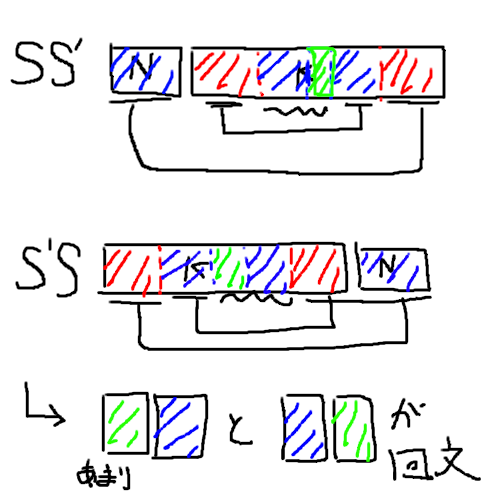
上の画像に示したように,あまりの周辺を考えるとは,「Sの逆順または正順と余った部分を左右に結合したもの」どちらもが回文をなすかどうかをチェックすればよいことになります。
場合分けが発生するというのは,K > Nと2N > Kで分けたのとちょうど同じような事情が発生するからです。したがって,
というようになります。この計算量は,Kがいくら多くてもざっくりO(N)に近いはずなので,おそらく大丈夫です。以上により,この問題を解くことができます。
実装例(C言語)
以下に私の実装例を示しますが,可読性をあまり考慮して書いていないので,実装に詰まったときの参考程度が良いと思います。
あとがき
今回新しい試みとして解説を作ってみましたが,改めて自分のアイデアを説明するということの難しさを実感します。また,画像の作成が思ったより面倒くさいので,競プロ勢の解説が短文+実装例だけになりがちなのはある程度しょうがないのかなとも思いました。
誤り,「ここが分からんからもっと細かく」等があれば Twitter のほうに連絡いただけると幸いです。ここまで読んでいただきありがとうございました。
前回の記事から気が付いたら一か月くらいかかってしまいましたが,ABCとかにはちゃんと参加しているのでこれからはまた参加記録毎週書こうかなと思っている所存です。それでは次の記事でお会いしましょう。