InTheDayDream

ABC330参加記録

Published on 2023-11-25
Last Modified 2023-11-25

Table Of Contents

はじめに

本稿は、2023-11-25に行われたABC330の参加記録です。 眠れない夜にはコンテストの参加記録を書くのが良いと古事記にも書いてあった要出典ので更新します。

戦績

今回の提出記録は以下の通りです。

AからEまでの5問正解できました。パフォーマンスは1420で、レーティング変動は1200→1224(+24)でした。

所感

今回解ける問題を解いたという感じです。 何とか緑落ち回避できてよかった。

雑振り返り

A - Counting Passes

問題へのリンク

配列を前からひとつづつ見ていけば良いです。 こういう感じのA問題楽でうれしいですよね。

import std;

void main () {
    int N, L; readln.read(N, L);
    int[] A = readln.split.to!(int[]);
    int count = 0;
    foreach (a; A) if (L <= a) count++;
    writeln(count);
}

void read (T...) (string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

B - Minimize Abs 1

問題へのリンク

Bにしては問題文が難しいです。何を言っているのかわからなくて1分くらい固まっていました。 要するに、次のような感じです。

$1 \leq i \leq N$に対して次の問題を解け。

これなら少しマシになった気がします。$A_i \in [L, R]$であれば、一番近い値は当然$A_i$そのものになるので、$A_i$が答えになります。 そうでない時は、$L$か$R$しかありえません。場合分けして解答しましょう。

import std;

void main () {
    int N, L, R; readln.read(N, L, R);
    int[] A = readln.split.to!(int[]);

    int[] ans = new int[](N);
    foreach (i, a; A) {
        if (L <= a && a <= R) {
            ans[i] = a;
        }
        if (a < L) ans[i] = L;
        if (R < a) ans[i] = R;
    }

    foreach (i, a; ans) write(a, i == ans.length-1 ? '\n' : ' ');
}

void read (T...) (string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

C - Minimize Abs 2

問題へのリンク

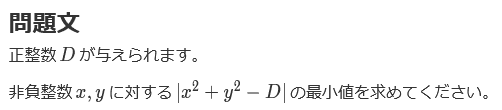
とりあえず$x$は固定して考えましょう。$D - x^2 = D^\prime$とおくと、$|y^2 - D^\prime|$の最小化問題になります。ただし、$D^\prime \in [D-1, \infty)$に留意しましょう。 うーん、絶対値記号が絶妙にキモいですね。多分外さなくてもいいはずですが、外しましょう。

$$\begin{equation*} |y^2 + D^\prime| = \max (y^2 - D^\prime, D^\prime - y^2) \end{equation*}$$

ムっ、この2項は単調性がありそうですね！ 1項目が最小になるときは、$D^\prime \leq y^2$を満たす最小の$y$で、2項目が最小になるときは、$y^2 \leq D^\prime$を満たす最大の$y$になるはずです。 これ、二分探索で求められそうですね。

というわけで、ある$x$を与えたときに、最適解になる$y$を高速に探索する方針がたったので、これで終わりです。

import std;

void main () {
    long D = readln.chomp.to!long;
    solve(D);
}

void solve (long D) {
    // xは10^6程度まででよいので、それらに対してyを探索

    long ans = long.max;
    long x = 1;
    while (true) {
        if (D < x*x) {
            break;
        }
        // このxに対してのyを求める -> 大体x^2+y^2 - D = 0 => x^2 + y^2 = D となるような感じで
        long ok = 0, ng = 2*10^^6;
        while (1 < abs(ok-ng)) {
            long mid = (ok+ng) / 2;
            if (x*x+mid*mid <= D) {
                ok = mid;
            } else {
                ng = mid;
            }
        }
        long candi = min(D - x*x - ok*ok, x*x + ng*ng - D);
        ans = min(ans, candi);
        x++;
    }

    writeln(ans);
}

void read (T...) (string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

$x$の上限が$\sqrt{D}$で抑えられることを考えれば、全体$O(\sqrt{D} \log \sqrt{D})$で抑えられているはずです。多分。 これは普通に難しいと思ったんですが、意外にdifficultyが低かったです。私の解よりもシンプルな全探索解が想定解法らしく(計算量も向こうの方が良い)ちょっと残念です。

D - Counting Ls

問題へのリンク

まず、行と列を固定して考えます。 そもそもこのような組が取れるのは、固定した行と列の交点がoであるもののみであることが分かります。 そこから、行と列の好きな場所から1つずつoをとればもれなく数え上げられそうです。 被りがないことの正当性は、固定した行と列が一つでも異なれば、角に当たる部分のoは必ず異なるものが採用されることから従います。 漏れがないことの正当性は、信じる気持ちです(は？)。

というわけで、各行と列に何個oがあるかを保持しておけば、グリッド走査分の$O(N^2)$で計算できます。 本番での私は意味不明なことをしていたので、upsolveの方をあげておきます。

import std;

void main () {
    int N = readln.chomp.to!int;
    string[] S = new string[](N);
    foreach (i; 0..N) S[i] = readln.chomp;

    solve(N, S);
}

void solve (int N, string[] S) {
    int[] vertical = new int[](N); // vertical[i] := 列iに何個'o'があるか
    int[] horizontal = new int[](N); // horizontal[i] := 行iに何個'o'があるか

    foreach (i; 0..N) foreach (j; 0..N) if (S[i][j] == 'o') horizontal[i]++;
    foreach (j; 0..N) foreach (i; 0..N) if (S[i][j] == 'o') vertical[j]++;

    long ans = 0;
    foreach (i; 0..N) foreach (j; 0..N) {
        if (S[i][j] == 'o') {
            ans += (horizontal[i]-1) * (vertical[j]-1);
        }
    }

    writeln(ans);
}

E - Mex and Update

問題へのリンク

一瞬セグメントツリーの香りを感じてビクッ！としましたが、落ち着いて考えます。 そもそもmex計算がややこしい点は、前の方の要素が全埋めされたときに、いきなり解が後ろの方に飛んでいくことがあり得るからです。 それなら、先に候補地を持っておけばよいじゃないという発想で解きました。

  1. 初期状態

mex候補は次のいずれかのみ。

  1. 更新

新しくmex候補となるのは次のいずれかのみ。

というわけで、実は候補地点は更新時に$O(1)$個しか変化しないんですね。 あとは雑に優先度付きキューに突っ込んで、mexとして採用できるかどうかは連想配列で判定したら解けます。

import std;

void main () {
    int N, Q; readln.read(N, Q);
    int[] A = readln.split.to!(int[]);
    solve(N, Q, A);
}

void solve (int N, int Q, int[] A) {
    // セグ木？ いや、実は候補が少ないパターンのやつだ
    // 新しく更新したとき、mex候補として一つ後ろをキューに積んでおけばよい

    int[int] mp;
    foreach (a; A) mp[a]++;

    BinaryHeap!(int[], "b<a") PQ = [];

    foreach (a; A) if (a+1 !in mp) PQ.insert(a+1);
    PQ.insert(0);

    int[] ans = new int[](Q);
    foreach (j; 0..Q) {
        int i, x; readln.read(i, x);
        i--;

        mp[A[i]]--;
        mp[x]++;
        if (x+1 !in mp || mp[x+1] == 0) PQ.insert(x+1);
        if (A[i] !in mp || mp[A[i]] == 0) PQ.insert(A[i]);
        A[i] = x;

        while (true) {
            auto head = PQ.front;
            if (head !in mp || mp[head] == 0) {
                ans[j] = head;
                break;
            }
            PQ.removeFront;
        }
    }

    foreach (a; ans) writeln(a);
}

void read (T...) (string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

最悪計算量の評価全くしてないけどなんか通りました。まあクエリが$2 \times 10^5$程度しか来ないので、それはそうですね。

また、この問題はもっと賢い解き方が存在します。$N$要素数列のmexは定義から$[0, N]$の区間内に入ります。 なので、実は極端に大きな項は無視してもよかったわけです。

この議論より、$0$から$N$までの$N+1$要素の配列を持ってシミュレーションをすると解けます。 mexを見つけるのは順序付き集合で対数時間です。

import std;

void main () {
    int N, Q; readln.read(N, Q);
    int[] A = readln.split.to!(int[]);
    solve(N, Q, A);
}

void solve (int N, int Q, int[] A) {
    int[] range = new int[](N+1); // [0, N]をシミュレーション
    auto rbt = new RedBlackTree!(int, "a<b", false);

    foreach (a; A) if (a <= N) range[a]++;
    foreach (i, r; range) if (r == 0) rbt.insert(cast(int) i);

    int[] ans = new int[](Q);
    foreach (j; 0..Q) {
        int i, x; readln.read(i, x);
        i--; // 0-indexed

        if (A[i] <= N) {
            range[A[i]]--;
            if (range[A[i]] == 0) rbt.insert(A[i]);
        }
        A[i] = x;
        if (x <= N) {
            range[x]++;
            if (range[x] == 1) rbt.removeKey(x);
        }

        ans[j] = rbt.front;
    }

    foreach (a; ans) writeln(a);
}

void read (T...) (string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

これ、とても賢いですね。mexは$[0, N]$というのは覚えておきたいです。

F - Minimize Bounding Square

問題へのリンク

難しい！正方形の1辺を二分探索するのかと思っていたけど、判定問題が全然解けない！ どうやら貪欲解も存在するらしく、まだまだ壁は高いなとおもいました。

終わりに

今回の参加記録はこれで終わりです。読んでいただきありがとうございました。 先週の参加記録を書けていなかったのが少し心残りです。 今週はいろいろと忙しくて、それをやるだけの心的余裕がありませんでした。

12月は緑以下オンサイトに行く予定です。もし行く人いたら仲良くしてください。そうでなければ多分ぼっちです。

昨日、MMA Contest 017がありましたが、実は私もテスターをさせていただきました。 走っていない人はぜひどうぞ。余裕があれば私も記事書きます(優先度低め)。

適当に近況も書いておきます。

この間のPG battleの景品が届きました。PG battleのステッカーが6枚も入っていてたまげたのですが、これあってますか？

最近kindleに興味があります。 先日、面白そうな本を見つけたのですが、経験上、本として所有していても読む機会がなかなかないなと思い、電子書籍なら読むのか実験してみたいという感じです。 基本食事中とかスマホばっかり見てるので、そういう時間に見れるブログみたいな本が読みたいな。とか妄想してます。ちなまだデビューしてないです。

いろいろと書き散らしたいことは脳内にあるのですが、いかんせん競技プログラミングのエントリ以外最初の一歩が踏み出せないのが悩みです (そういうアイディアは形にしようとすると崩壊するのが常なので、まあそれはそうという感じかも)。

それではまた。

Tags for this post: 競技プログラミング コンテスト参加記録

Other posts tagged by "競技プログラミング"

more ...

Other posts tagged by "コンテスト参加記録"

more ...
Power by Hugo / Theme simplog by michimani