ABC328参加記録
Published on 2023-11-12Last Modified 2023-11-12
Table Of Contents
はじめに
本稿は、2023-11-11に行われた ABC328 の参加記録です。
戦績
今回の提出は以下の通りでした。
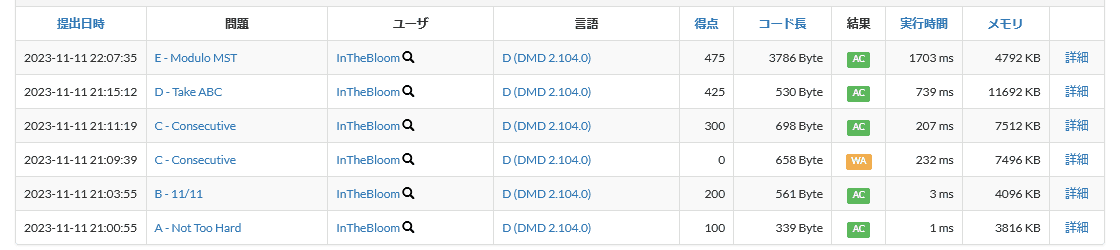
AからEの5問正解できました。 今回のレーティング変動は以下の通りでした。
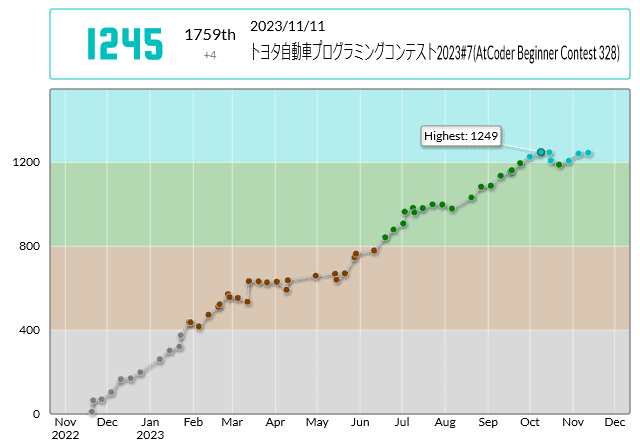
パフォーマンスは1281で、 レーティング変動は1241→1245(+4) でした。
所感
今回はDまでかなり早く解ましたがE問題で詰まってしまい、パフォーマンスがあまり伸びませんでした。 解けないとマズいという問題は解けたので、とりあえず良しとします。
今回のF問題がPotentialized UnionFindというものを利用すれば簡単に解けたらしく、 自分が解法にたどり着けなかったという点と、ちゃんと前もって学習できていなかったということに対してかなり悔しく感じてします。 今週のプロコンは、このデータ構造を理解してD言語による実装を与えることを目標にやろうかなと思います。
学ぶ機会をもらったと思って頑張ります。
問題振り返り
A - Not Too Hard

最近のA問題の中でも結構簡単な方な気がします。配点をひとつづつ見ていって、X以下なら足しましょう。
import std;
void main () {
int N, X; readln.read(N, X);
int[] S = readln.split.to!(int[]);
int ans = 0;
foreach (s; S) if (s <= X) ans += s;
writeln(ans);
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
B - 11/11

実装を考えるとき、有効な月/日を生成することと、ゾロ目になることを分けて考えるとやりやすいのかなと思います。
型変換(int -> string)を簡単にできる言語なら、次のような実装がよいかと思います。
import std;
void main () {
int N = readln.chomp.to!int;
int[] D = readln.split.to!(int[]);
int ans = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= D[i-1]; j++) {
auto S = i.to!string ~ j.to!string;
bool ok = true;
foreach (s; S) if (s != S[0]) ok = false;
if (ok) ans++;
}
}
writeln(ans);
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
そうでない言語なら、判定部分を
bool ok = true;
int basis = i%10;
while (0 < i) {
if (i%10 != basis) ok = false;
i /= 10;
}
while (0 < j) {
if (j%10 != basis) ok = false;
j /= 10;
}
という感じになるかなと思います。
C - Consecutive

ナイーブに操作すると$r_i - l_i$が大きいクエリばかり飛んでくるときが最悪ケースで、$O(N^2)$です。
区間クエリを高速化する問題は、累積和を考えると良い場合があります。この問題はまさにそうで、
cum[i] := (S[j] == S[j+1]なら1、そうでないなら0 の 0<=j<=iの総和)と定めると、
前処理$O(N)$クエリ$O(1)$で答えることができます。
クエリをどうやって処理するべきかを一回考えると思いつきやすいような気がします。
(連続区間において条件を満たす場所を数える) -> (条件を満たす場所を1、満たさない場所を0と対応させて、Static Range Sum Queryに帰着) -> 累積和 という流れなのかなと思います。
2番目の考察(あるを1、ないを0に対応させること)がかなりad-hocな気がしますが、これはかなり頻出なので覚えるべきことなのかな?
ちなみに、2番目の考察はDynamic Kth Elementとか$O(N \log N)$の転倒数にも現れるアイデアです。
import std;
void main () {
int N, Q; readln.read(N, Q);
string S = readln.chomp;
solve(N, Q, S);
}
void solve (int N, int Q, string S) {
// imosをやる
long[] cum = new long[](N);
foreach (i; 0..S.length-1) if (S[i] == S[i+1]) cum[i]++;
foreach (i; 1..N) cum[i] += cum[i-1];
foreach (_; 0..Q) {
int l, r; readln.read(l, r);
l--, r--;
if (l == r) { writeln(0); continue; }
if (0 < l) writeln(cum[r-1]-cum[l-1]);
else writeln(cum[r-1]);
}
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
D - Take ABC

ナイーブに操作すると削除の後に「詰める」操作が発生するので、$O(N^2)$になります。これを改善します。
「左から削除していく」という文言を見た時点で、括弧列の対応を見る問題との共通点を感じました。
"ABC"が"()"だったら有効括弧列を消す問題になるんじゃないかな?
括弧列の問題 ->
文字列を先頭から見ていって(見たやつをスタックに積んでいって)
")"が出てきたらスタックの先頭が"("かどうかチェックする。
この問題 ->
文字列を先頭から見ていって"C"が出てきたらスタックの先頭が"AB"かどうかチェックする。
みたいな感じで処理できます。一つの文字を高々2回までしか参照しないので、$O(N)$です。
import std;
void main () {
string S = readln.chomp;
solve(S);
}
void solve (string S) {
/* 前から見ていけばよろしい */
char[] ans;
foreach (c; S) {
ans ~= c;
if (3 <= ans.length) {
if (ans[$-3..$] == "ABC") {
ans = ans[0..$-3];
}
}
}
writeln(ans);
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
E - Modulo MST

全域木(Spanning Tree)とは、与えられた$G$の部分グラフ$G’$であって、$G$のすべての頂点$V(G)$を含み、かつ木であるようなものをいいます。
全域木であって、辺の重みの総和が最小であるものを最小全域木(MST)といいますが、本問では総和ではなく総和を$K$で割ったあまりをコストとしています。 最小全域木を求めるアルゴリズム(クラスカル法など)は役に立ちそうにないです。
制約を見ると、不自然に小さいです。また、あまりを含む最小化問題は感覚的に全探索しかなさそうな感じがします。 そこで、全探索を考えましょう。
「$G’$が全域木である」 ならば 「$G’$は$N-1$本の辺を持つ」 は真です。つまり、 $G$が全部で$M$本の辺を持つ時、 $\dbinom{M}{N-1}$通りの辺の取り方を全部調べることができたら十分なことは明らかです。 (この組み合わせには全域木にならないケースも含まれる可能性がありますが、それはコスト更新の時に無視したらよいです。)
今回に関しては最大ケースで$\dbinom{28}{7} = 1184040$になります。これで通せそうです。
import std;
struct trio {
int u, v;
long w;
}
void main () {
int N, M;
long K;
readln.read(N, M, K);
trio[] edge = new trio[](M);
foreach (i; 0..M) with(edge[i]) {
readln.read(u, v, w);
u--, v--;
}
solve(N, M, K, edge);
}
void solve (int N, int M, long K, trio[] edge) {
/* Nが十分に小さいので、あり得る全域木を全探索すればよろしい */
/* ほげほげのコストを無視すれば、ありうる全域木は28C7 ~ 10^6通りのはず */
/* あほか?28C7列挙すればいいだろう */
int[][] graph = new int[][](N, 0);
bool[] visited = new bool[](N);
bool check (trio[] edge) {
foreach (ref g; graph) g.length = 0;
foreach (e; edge) {
graph[e.u] ~= e.v;
graph[e.v] ~= e.u;
}
visited[] = false;
void dfs (int pos) {
visited[pos] = true;
foreach (to; graph[pos]) {
if (!visited[to]) dfs(to);
}
}
dfs(0);
foreach (v; visited) if (!v) return false;
return true;
}
long ans = long.max;
foreach (e; enumComb(edge, N-1)) {
if (check(e)) {
long sum = 0;
foreach (ee; e) (sum += ee.w) %= K;
ans = min(ans, sum);
}
}
writeln(ans);
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
struct enumComb_(T) {
import std.exception;
import std.format;
import std.range.primitives : ElementType, isRandomAccessRange;
long N, K;
long[] idx;
bool isEmpty;
enum bool isNumeric = __traits(isIntegral, T);
static if (!isNumeric) {
static assert(__traits(compiles, isRandomAccessRange!(T)) || is(T == E[n], E, size_t n) || is(T == E[], E),
"T must be Integral type or RandomAccessRange. Now T = ", T.stringof);
alias E = ElementType!(T);
E[] res;
T arr;
}
this (T N, long K) {
static if (isNumeric) {
auto msgN = format("Line : %s, N must be greater than or equal to 0. your input = %s", __LINE__, N);
enforce(0 <= N, msgN);
this.N = N;
} else {
this.N = N.length;
arr = N;
res = new E[](cast(uint) K);
}
auto msgK = format("Line : %s, K must be greater than or equal to 0. your input = %s", __LINE__, K);
enforce(0 <= K, msgK);
this.K = K;
idx = new long[](cast(uint) K);
init();
}
void init () {
foreach (i; 0..K) {
idx[cast(uint) i] = i;
}
if (N < K) {
isEmpty = true;
}
}
bool empty() const {
return isEmpty;
}
static if (isNumeric) {
long[] front() {
return idx;
}
} else {
E[] front () {
foreach (i, x; idx) {
res[i] = arr[cast(uint) x];
}
return res;
}
}
void popFront() {
long index;
(){
foreach (i; 0..K) {
if (idx[cast(uint) ($-i-1)] < N-i-1) {
idx[cast(uint) ($-i-1)]++;
index = K-i-1;
return;
}
}
// there is no choice :(
isEmpty = true;
}();
foreach (i; index+1..K) {
idx[cast(uint)i] = idx[cast(uint)i-1] + 1;
}
}
}
auto enumComb(T) (T N, long K) {
return enumComb_!(T)(N, K);
}
ちょうど$\dbinom{N}{K}$を列挙するアルゴリズムを用意していたので、そんなに苦労せず実装できました。 1700msだったのであまりよくない実装をしていたっぽい…?
F - Good Set Query

題意自体はつかめたのですが、いつものトポロジカル順に処理する奴ではうまく列$(X_1, X_2, \dots, X_N)$ を決められないなーと思い、そこで行き詰りました。
どうやら重み付き(ポテンシャル付き)UnionFindなるデータ構造で解けるようです。 今週中に解法及びデータ構造を理解して、ACします。(時間があれば別記事たてます。)
終わりに
書きたいことは大体書いたので、あとは適当に近況でも書きます。
最近レーティングが1200あたりで収束している感じがあり、上に行くためにはもっとプロコンに力を入れないとなーと感じています。もっといろんな知識を仕入れたいです。 短期的な目標としては来年までに1300到達、もう少し長期的な目標は次のICPCまでに1600到達です。 無理かもしれませんが、Problemsの水色埋めを客観的に見た感じ到達可能にも感じます。
あと、思うこととして、レーティングとかの指標は本来過去の自分と比較すべきだと考えているのですが、 Twitterとかを追っていると意味のない焦りや嫉妬によって無駄なエネルギーが消耗している実感があります。本来こんな無駄なことをせずに研鑽すべきなんですがね。。。 過去の経験も含めて自分はSNS依存の傾向があるので、自制していきたいですね。
最近、品田遊著「名称未設定ファイル」 Amazonリンク(アフィではないです) を読みました。 星新一が好きな人とかおすすめです。あと、普段本じゃなくてネットばっかり見てる私みたいな人にもおすすめです。
それではこのあたりにしておこうと思います。また次のエントリで。