ABC327参加記録

Published on 2023-11-05
Last Modified 2023-11-05

Table Of Contents

はじめに

本稿は、2023-11-04に行われたABC327の参加記録です。

戦績

今回の提出状況は次の通りです。

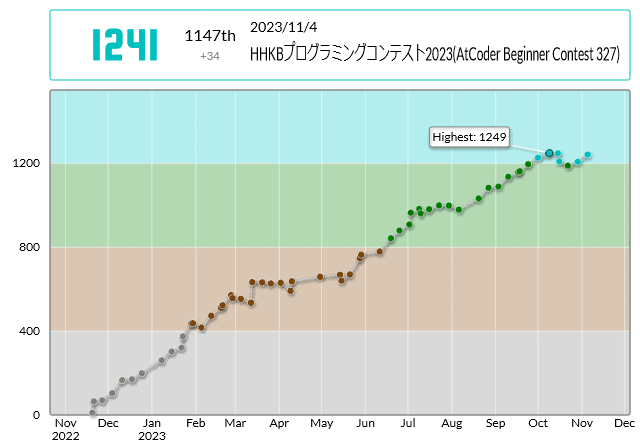
AからEまでの5問正解できました。パフォーマンスは1513で、レーティング変化は1207→1241(+34)でした。

所感

今回は割と早解きできた回だったかなという感じです。 5問目は割と非自明だと思ったのですがかなりたくさんの人が通していました。とりあえず緑色に再び落下しなくてほっとしています。

問題雑振り返り

A - ab

問題へのリンク

Nが十分に小さいため、全部ナイーブに見ていくことで十分ACできます。最初勘違いしていたため、サンプルに"ba"の順でYesが出るものがあってよかったです。

import std;

void main () {
    int N = readln.chomp.to!int;
    string S = readln.chomp;
    foreach (i; 0..S.length-1) {
        if ((S[i] == 'a' && S[i+1] == 'b') ||
            (S[i] == 'b' && S[i+1] == 'a')) {
            writeln("Yes");
            return;
        }
    }
    writeln("No");
}

void read(T...)(string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

B - A^A

問題へのリンク

$A^A$はかなり急激に大きくなるので、$A$を1から順番に$A^A$が$B$を超えるまで増やしていけばよさそうです。実際、$10^{18} < 16^{16} = 18446744073709551616$なので、$A = 15$までを調べればよいです。

import std;

void main () {
    long B = readln.chomp.to!long;
    for (long A = 1; ; A++) {
        if (B < A^^A) {
            writeln(-1);
            return;
        }
        if (B == A^^A) {
            writeln(A);
            break;
        }
    }
}

void read(T...)(string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

ちなみに私の提出は通ってはいるものの、かなりまずいことをしています。というのも、long.maxよりも$16^{16}$のほうが大きいためオーバーフローしています。しかし、偶然オーバーフローを含めて$10^{18} < A^A$となるAが存在するようです。ちゃんとACをとる場合はA=15で止めるか多倍長整数を使うと良いです。

C - Number Place

問題へのリンク

条件1と条件2は二重ループで簡単に判定できます。条件3は少し複雑ですが、3×3領域を9回判定すると考えると比較的楽に判定をつくれます。具体的には3×3領域のスタート地点(0, 0), (0, 3), (0, 6), …, (6, 6)をループで列挙して、判定自体はつかいまわします。

import std;

void main () {
    int[][] A = new int[][](9, 0);
    foreach (i; 0..A.length) A[i] = readln.split.to!(int[]);

    solve(A);
}

void solve (int[][] A) {
    bool isOk = true;
    int[] mp = new int[](10);

    /* 条件1 */
    foreach (i; 0..A.length) {
        mp[] = 0;
        foreach (j; 0..A[i].length) {
            mp[A[i][j]]++;
        }
        foreach (k; 1..10) {
            if (mp[k] != 1) isOk = false;
        }
    }

    /* 条件2 */
    foreach (j; 0..A[0].length) {
        mp[] = 0;
        foreach (i; 0..A.length) mp[A[i][j]]++;
        foreach (k; 1..10) {
            if (mp[k] != 1) isOk = false;
        }
    }

    /* 条件3 */
    int SY, SX;

    SY = 0;
    foreach (_; 0..3) {
        SX = 0;
        foreach (__; 0..3) {
            /* 処理 */
            mp[] = 0;
            foreach (i; 0..3) foreach (j; 0..3) {
                int y = SY + i;
                int x = SX + j;
                mp[A[y][x]]++;
            }
            foreach (k; 1..10) {
                if (mp[k] != 1) isOk = false;
            }

            SX += 3;
        }
        SY += 3;
    }

    if (isOk) {
        writeln("Yes");
    } else {
        writeln("No");
    }
}

void read(T...)(string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

D - Good Tuple Problem

問題へのリンク

二つの数列によってXの2項間に制約が課されていきます。経験上、数列に制約を課していくような問題はグラフ表現に置き換えられないかを検討すると解けることがあります。この問題はその方針さえ引ければかなり見えやすいと思います。要はA[i]項目とB[i]項目が違えばよいので、 A[i]項目とB[i]項目の間に無向辺を張ったときに全体が二部グラフを成せばよいです。

二部グラフの判定にUnionFindを使えるらしいですが、よく理解していないので普通にdfsしました。

import std;

void main () {
    int N, M; readln.read(N, M);
    int[] A = readln.split.to!(int[]);
    int[] B = readln.split.to!(int[]);

    solve(N, M, A, B);
}

void solve (int N, int M, int[] A, int[] B) {
    /* グラフ表現に落とし込んで解く */
    /* 要は二部グラフなら良い */
    A[] -= 1; B[] -= 1;
    int[][] graph = new int[][](N, 0);
    foreach (i; 0..M) {
        graph[A[i]] ~= B[i];
        graph[B[i]] ~= A[i];
    }

    int[] visited = new int[](N);
    visited[] = -1;
    bool isOk = true;

    void dfs (int pos) {
        foreach (to; graph[pos]) {
            if (visited[to] == -1) {
                if (visited[pos] == 0) visited[to] = 1;
                if (visited[pos] == 1) visited[to] = 0;
                dfs(to);
            } else {
                /* 矛盾がないか判定 */
                if (visited[pos] == visited[to]) isOk = false;
            }
        }
    }

    foreach (i; 0..N) {
        if (visited[i] == -1) {
            visited[i] = 0;
            dfs(i);
        }
    }

    if (isOk) {
        writeln("Yes");
    } else {
        writeln("No");
    }
}

void read(T...)(string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}

E - Maximize Rating

問題へのリンク

式をぐっとにらむところから考察スタートしました。 kがいろいろな値をとると面倒くさいので、とりあえず固定して考えます。すると、$\sum_{i=1}^{k} (0.9)^{k-i} Q_i$を最大化する問題になります。が、変な係数がかかっているせいでQは貪欲にとれそうにありません。どうしましょう。

貪欲に取れない状況下で最適な部分集合を選ぶ問題というのは基本的に「全部見る」しかないはずです。なので、この段階でdp濃厚だなーという感じです。(もちろん違う方針なときもあります。)

ここで天啓が訪れます。パフォーマンス$P_i$をx番目の項として採用する場合、それまでにx-1個を採用した部分集合のみを考えればよいはずです。この方針で状態を圧縮します。

あとからとった項が前にとった項に直接寄与することがないので、次のdpができます。

$$ dp[i][j] = (Pを逆から見て、i項目までにj項とったときの\sum (0.9)^{k-i} Q_iの最大値) $$

遷移は

/* 採用 */
dp[i+1][j+1] = dp[i+1][j+1], dp[i][j] + P[N-i-1]\*pow(0.9, j));

/* 採用しない */
dp[i+1][j] = max(dp[i+1][j], dp[i][j]);

となります。

このようなdpを私は勝手に「とる/とらないdp」と呼んでいるのですが、圧縮後の値に部分集合の何項目に採用されたかという情報ものせられるのかと勉強になりました。

import std;

void main () {
    int N = readln.chomp.to!int;
    int[] P = readln.split.to!(int[]);
    solve(N, P);
}

void solve (int N, int[] P) {
    /* いくつとるかを定めると、あとは最適なPの部分集合を見つける作業になる。 */
    /* 最近のものほど重みが高い... -> 最適な部分集合は変わりうる。 */
    /* 逆から考えれば、i項目まで見て、j個とって...とすると最適解をタプルに縮退できる。 */
    /* dpをしましょう。 */

    double[][] dp = new double[][](N+1, N+1);
    // dp[i][j] := 逆からi項目まで見て、j個とったとき、ありうる最大の分子

    foreach (d; dp) d[] = -1;
    dp[0][0] = 0;

    foreach (i; 0..N) foreach (j; 0..N) {
        if (0 <= dp[i][j]) {
            // とる
            dp[i+1][j+1] = max(dp[i+1][j+1], dp[i][j] + P[$-i-1]*pow(0.9, j));
            // とらない
            dp[i+1][j] = max(dp[i+1][j], dp[i][j]);
        }
    }

    double[] denominators = new double[](N+1);
    denominators[] = 0;
    denominators[1] = 1;
    foreach (i; 2..N+1) denominators[i] = denominators[i-1] + pow(0.9, i-1);

    double ans = -double.max;
    foreach (i; 0..N+1) foreach (j; 0..N+1) {
        if (0 < j) {
            ans = max(ans, dp[i][j]/denominators[j] - (1200/sqrt(j.to!double)));
        }
    }

    writefln("%.10f", ans);
}

void read(T...)(string S, ref T args) {
    auto buf = S.split;
    foreach (i, ref arg; args) {
        arg = buf[i].to!(typeof(arg));
    }
}