ABC322参加記録
Published on 2023-09-30Last Modified 2023-09-30
Table Of Contents
はじめに
本稿は、2023/09/30に行われた ABC322 の参加記録です。
戦績
今回の提出状況は次の通りです。
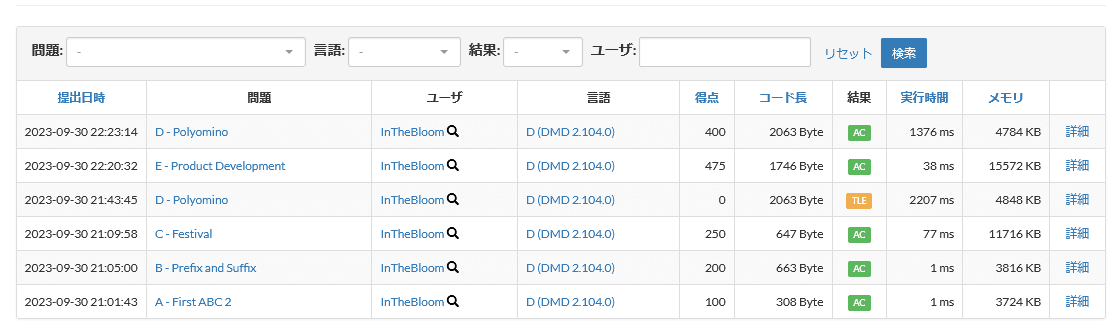
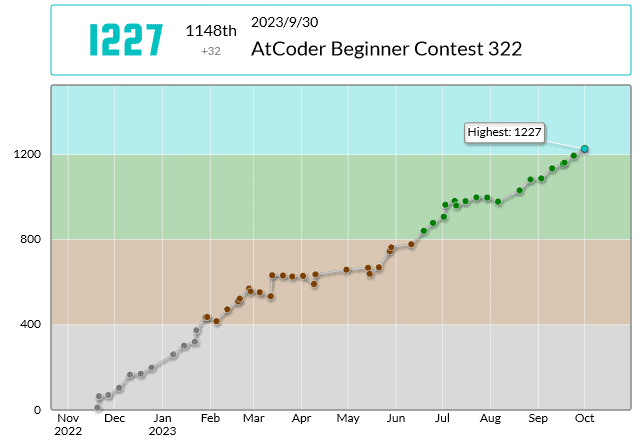
AからDまでの5完でした。パフォーマンス1480で、レーティング変化は1195 => 1227でした。
所感
遂に水色乗れました。うれしいです。
今回はDEがかなり実装が大変でした。 D問題TLEしてしまって、あきらめそうになりましたが、定数倍高速化をいろいろやってみたら通りました。
E問題はあまり賢くない実装方針をとってしまいかなり大変でしたが、何とか通せてよかったです。
解法
A - First ABC2

nの定義域が明示されているのは楽でいいですね。 前から力任せ法で見ていけば十分高速です。
スライスがある言語なら、スライスを用いるとちょっと楽かもしれないです。
import std;
void main () {
int N = readln.chomp.to!int;
string S = readln.chomp;
solve(N, S);
}
void solve (int N, string S) {
foreach (i; 0..S.length-2) {
if (S[i..i+3] == "ABC") {
writeln(i+1);
return;
}
}
writeln(-1);
}
B - Prefix and Suffix

SがTの接頭辞であるかどうか?とSがTの接尾辞であるか?を判定する方法があればif文で解けます。 N、Mは十分小さい上、制約でSの長さはT以下であることが保証されているので、全部言われたとおりに見ていけばよいです。
実装ではスライスを用いていますが、普通にfor文回しても解けます。 この場合、関数化するとちょっと楽だと思います。
import std;
void main () {
int N, M; readln.read(N, M);
string S = readln.chomp;
string T = readln.chomp;
solve(N, M, S, T);
}
void solve (int N, int M, string S, string T) {
int ans = 3;
if (S.length <= T.length && T[0..S.length] == S && T[$-S.length..$] == S) ans = 0;
if (S.length <= T.length && T[0..S.length] == S && T[$-S.length..$] != S) ans = 1;
if (S.length <= T.length && T[0..S.length] != S && T[$-S.length..$] == S) ans = 2;
writeln(ans);
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
C - Festival

二分探索を用いてi<=Ajが初めて成立するポイントを探します。 AM=Nなので、境界を多少雑に扱っても解けます。
普段ならAM<iである可能性があるので、判定関数をA[M<x]=infとするのですが、今回は必要ないです。
import std;
void main () {
int N, M; readln.read(N, M);
int[] A = readln.split.to!(int[]);
solve(N, M, A);
}
void solve (int N, int M, int[] A) {
bool f (int i, int x) {
return i <= A[x];
}
for (int i = 1; i <= N; i++) {
int ok = M-1, ng = -1;
while (1 < abs(ok-ng)) {
int mid = (ok+ng)/2;
if (f(i, mid)) ok = mid;
else ng = mid;
}
writeln(A[ok]-i);
}
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
D - Polyomino

少し大きな台紙を用意して、はみだし、かぶりのないように張り付けて条件を満たすかを見ていく全探索をしました。 3つあるミノのうちの1つは向きを固定してよいため、そこで少し高速化しています。
1300msかかってるの私だけっぽいので、もう少しマシな解き方を復習しようかなと思います。
import std;
void main () {
char[][][] mino = new char[][][](3, 4, 0);
foreach (i; 0..3) foreach (j; 0..4) mino[i][j] = readln.chomp.dup;
solve(mino);
}
void solve (char[][][] mino) {
char[][] field = new char[][](12, 12);
void AllClear () {
foreach (ref f; field) f[] = '.';
}
bool isOver () {
foreach (i, ff; field) foreach (j, f; ff) {
if (f == '#' && (i < 4 || 8 <= i || j < 4 || 8 <= j)) return true;
}
return false;
}
bool paste (int idx, int i, int j) {
foreach (y; i..i+4) foreach (x; j..j+4) {
if (mino[idx][y-i][x-j] == '.') continue;
if (mino[idx][y-i][x-j] == '#' && field[y][x] == '#') return false;
if (mino[idx][y-i][x-j] == '#' && (y < 4 || 8 <= y || x < 4 || 8 <= x)) return false;
if (mino[idx][y-i][x-j] == '#' && field[y][x] == '.') field[y][x] = '#';
}
//return !isOver();
return true;
}
bool check () {
int count = 0;
foreach (i, ff; field) foreach (j, f; ff) if (f == '#') count++;
return count == 16;
}
// 始点縦と横
foreach (i1; 0..7) foreach (j1; 0..7) {
// 1ピースは向き確定でもよい。
//foreach (_1; 0..4) { mino[0] = mino[0].rotate;
foreach (i2; 0..7) foreach (j2; 0..7) foreach (_2; 0..4) {
mino[1] = mino[1].rotate;
foreach (i3; 0..7) foreach (j3; 0..7) foreach (_3; 0..4) {
mino[2] = mino[2].rotate;
AllClear();
if (paste(0, i1, j1) && paste(1, i2, j2) && paste(2, i3, j3) && check()) {
writeln("Yes");
return;
}
}
}
}
writeln("No");
}
char[][] rotate (char[][] X) {
if (X.length == 0) return [];
char[][] res = new char[][](X[0].length, X.length);
foreach (i; 0..X.length) foreach (j; 0..X[i].length) res[$-j-1][i] = X[i][j];
return res;
}
E - Product Development

こういうのは大抵貪欲は無理だと相場が決まっています。また、とるかとらないかのO(2N)全探索もNが少し大きすぎます。
そこで、パラメータの取りうる値が小さいことに着目します。 一つのパラメーターに対して、P以上になったものはすべて同一視してよいため、本質的に区別すべき状態はパラメーターがP未満のもののみです。
いくつかの開発案を採択したとき、ありうる状態はパラメーター1つあたり0からPまでのP+1通りになり、パラメーターがK個独立に存在するので、(P+1)K通りになります。 これを持ちながら多次元部分和問題のようなことをやります。
私は全ケースK=5に帰着させて解きました。具体的には、K<jであってAi,jが存在しない時、Ai,j=Pと定義してあります。 こうすることで、本来存在しない架空のパラメータを一つ以上の開発案をとれば必ず達成できるとみなしています。
こういうdpは、多次元空間をイメージするよりも「ノードの識別子(一意に特定するために必要なタグ)がK種類ある」という理解が良いと思います。
一応この手のdpは過去にたくさん出題例があります。 その一部を紹介します。
import std;
void main () {
int N, K, P; readln.read(N, K, P);
int[] C = new int[](N);
int[][] A = new int[][](N, 0);
foreach (i; 0..N) {
int[] input = readln.split.to!(int[]);
C[i] = input[0];
A[i] = input[1..$];
}
solve(N, K, P, C, A);
}
void solve (int N, int K, int P, int[] C, int[][] A) {
long[][][][][][] dp = new long[][][][][][](N+1, P+1, P+1, P+1, P+1, P+1);
// dp[i][j][k][l][m] := (i, j, k, l, m)を達成できる最小コスト(ただし、パラメータ=5は達成できている)
foreach (dim; 0..N+1) foreach (i; 0..P+1) foreach (j; 0..P+1) foreach (k; 0..P+1) foreach (l; 0..P+1) dp[dim][i][j][k][l][] = long.max;
dp[0][0][0][0][0][0] = 0;
int f (int[] a, int idx) {
if (idx < a.length) return a[idx];
return P;
}
foreach (dim, a; A) foreach (i; 0..P+1) foreach (j; 0..P+1) foreach (k; 0..P+1) foreach (l; 0..P+1) foreach (m; 0..P+1) {
if (dp[dim][i][j][k][l][m] == long.max) continue;
// とる
dp[dim+1][min(f(a, 0) + i, P)][min(f(a, 1) + j, P)][min(f(a, 2) + k, P)][min(f(a, 3) + l, P)][min(f(a, 4) + m, P)] = min(dp[dim][i][j][k][l][m] + C[dim], dp[dim+1][min(f(a, 0) + i, P)][min(f(a, 1) + j, P)][min(f(a, 2) + k, P)][min(f(a, 3) + l, P)][min(f(a, 4) + m, P)]);
// とらない
dp[dim+1][i][j][k][l][m] = min(dp[dim+1][i][j][k][l][m], dp[dim][i][j][k][l][m]);
}
if (dp[N][P][P][P][P][P] == long.max) {
writeln(-1);
} else {
writeln(dp[N][P][P][P][P][P]);
}
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
急いで解いたので、一部コメントが間違っています。そもそももう少しましな方針があるので、そちらを参考にすべきです。
終わりに
最近レーティングに取り憑かれている実感があったので、とりあえず水色に乗って一区切りつけることができてよかった。
純粋にProblem Solvingを楽しめるように努力したいと思った。プロコンを嫌いにならないためにも。