ABC321参加してきた。
Published on 2023-09-23Last Modified 2023-09-23
Table Of Contents
久しぶりに参加記録を書きます。
ここ1か月くらい参加記録をずっとさぼっていましたが、hugoに移行したことでだいぶん楽になったので今週はちゃんと書きます。
本稿は ABC321 の参加記録です。
戦績
今回の提出は以下の通りでした。
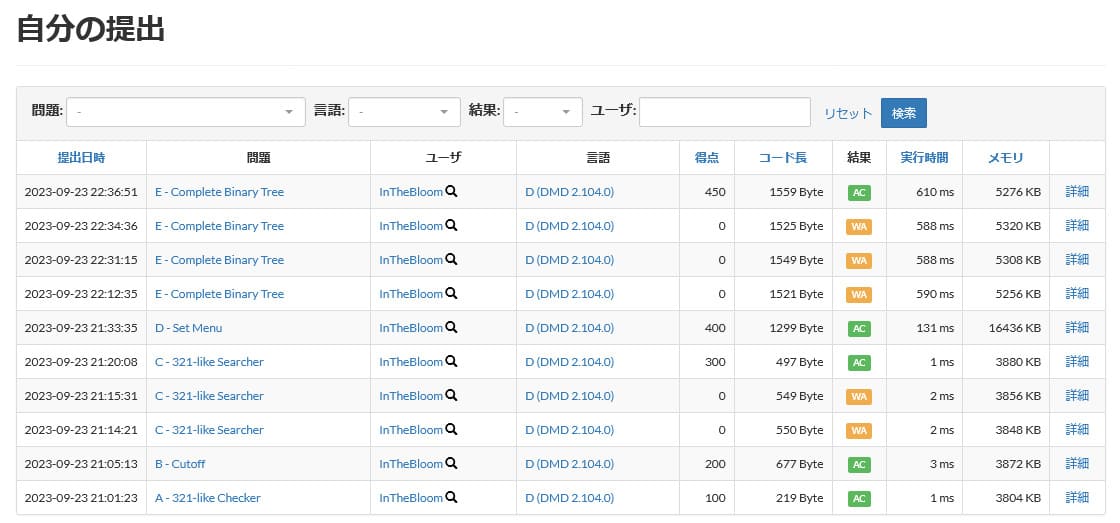
今回AからEの5問解くことができました。
所感
今回はD問題まではさっと解法が見えました。 C問題は以前にABCの 過去問 で広義単調増加列の全探索をしたことがあったので、パッと見た瞬間に全列挙可能だと分かりました。
E問題はエーッ!やりたくないです!みたいな見た目をしていたが、こういう時に後ろの問題を見に行っていいことがあったためしがないので頑張って取り組みました。
雑振り返り
A - 321-like Checker
問題文

書いてある通りにチェックしたらOKです。こういう時は文字列として受け取ると楽です。
import std;
void main () {
string N = readln.chomp;
foreach (i; 0..N.length-1) {
if (N[i] <= N[i+1]) {
writeln("No");
return;
}
}
writeln("Yes");
}
B - Cutoff
問題文

制約がデカければ面倒くさそうですが、実は簡単な全探索が通ります。 Nラウンド目に0から100点のどれかしか取れないので、最終結果としてあり得るものは高々100通りです。
よって、これらすべてについて問題文の通りにチェックを入れると解けます。 「全部見る」ということで複雑さを全部破壊するのは気持ちよいですね。
import std;
void main () {
int N, X; readln.read(N, X);
int[] A = readln.split.to!(int[]);
int[] B;
int ans = int.max;
for (int i = 0; i <= 100; i++) {
B = A.dup;
B ~= i;
B.sort;
int score = 0;
for (int j = 1; j < B.length-1; j++) {
score += B[j];
}
if (X <= score) {
ans = min(ans, i);
}
}
if (ans == int.max) {
writeln(-1);
} else {
writeln(ans);
}
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
C - 321-like Searcher
問題文

実は以前もう少し緩い制約で定義される数を探索する問題を解いたことがあって、その時の記憶が残っていたので即座に全探索の判断をとりました。 上の桁から決めていくような感じでdfsで掘りました。 重複とか怖かったので一応対策しています。
1WAでペナってしまったので、おそらくオーバーフローかな?
import std;
void main () {
int K = readln.chomp.to!int;
solve(K);
}
void solve (int K) {
// 狭義単調減少列は少なかったような気がするので全列挙します。
long[] number;
void dfs (long current, int last) {
for (int i = 0; i < last; i++) {
dfs(10*current+i, i);
}
if (0 < current) number ~= current;
}
dfs(0, 10);
number = number.sort.uniq.array;
writeln(number[K-1]);
}
D - Set Menu
問題文

こういうのは大抵片方を固定するとよいと相場が決まっています。
実際、この問題においてA[i]を一つ固定すると、必ず和がPを超えるかどうかで境界線を引くことができます。
これを二分探索します。
いちいちBの総和をとっているとO(M^2)が乗ってくるので、累積和で1ケースO(1)に落とします。
import std;
void main () {
int N, M, P; readln.read(N, M, P);
int[] A = readln.split.to!(int[]);
int[] B = readln.split.to!(int[]);
solve(N, M, P, A, B);
}
void solve (int N, int M, int P, int[] A, int[] B) {
// Aを一つ決めたときに境界線を探す。
long ans = 0;
B.sort;
long[] cum; cum.reserve(M+1);
cum ~= 0;
foreach (b; B) {
cum ~= cum[$-1]+b;
}
long f (int idx) {
if (idx < 0) return cast(long) -int.max;
if (M <= idx) return cast(long) int.max;
return B[idx];
}
foreach (a; A) {
// 二分探索: a+f(ok) <= P, P < a+f(ng)
// ただし、f(x<0)=-inf, f(M<=x)=inf
int ok = -1, ng = M;
while (1 < abs(ok-ng)) {
int mid = (ok+ng) / 2;
if (a+f(mid) <= P) {
ok = mid;
} else {
ng = mid;
}
}
if (ok == -1) {
ans += 1L*P*M;
} else {
ans += 1L*(ok+1)*a+cum[ok+1];
ans += 1L*P*(M-ok-1);
}
}
writeln(ans);
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
一発で通せて本当に良かった。
E - Complete Binary Tree
問題文

制約は載せていませんが、Tが105で、そのほか1018です。 まず、この木がどうなっているのかを図に書いてチェックします。 すると、これは完全二分木になっていることが確かめられます。
さて、制約がクソでかなので、グラフ上で実際にチェックしてやるのは無理です。 完全二分木の何かしらの性質を使います。
しばらく悩んで、例えばX=1で固定だったらどうだろうという発想に至りました。
この時、割と簡単に解けそうだなという感じです。具体的には、最左のノードと最右のノードの番号を持っておいて、(left, rightとします。)
left = 2*left;
right = 2*right+1;
を深さ分だけ続けていけばよさそうです。
途中でN < leftなら解は0で、そうでなければmin(N, right)-left+1になりそうな感じです。
式で書くと分かりにくいですが、実際はずっと15要素の二分木とにらめっこしていました。
というわけで、自分を根とする部分木に対してなら問題が解けました。
頂点1以外は必ず親を持つので、この部分木に対する問題を解くサブルーチンを適切に親ノードを選んで実行する感じで解きました。
import std;
void main () {
int T = readln.chomp.to!int;
foreach (_; 0..T) {
long N, X, K; readln.read(N, X, K);
long ans = solve(N, X, K);
writeln(ans);
}
}
long solve (long N, long X, long K) {
// 自分を根とする部分木の数え上げはできそう
/* return: 自分を根とする部分木において、自分との距離がdistであるようなものの数を数え上げる。多分logくらい */
long count (long root, long dist) {
enforce(0 <= dist);
if (N < root) return 0;
if (dist == 0) return 1L;
long left = root, right = root;
while (0 < dist) {
left = 2*left;
right = 2*right+1;
dist--;
if (N < left) return 0;
}
return min(N, right)-left+1;
}
bool[long] memo;
long ans = 0;
ans += count(X, K);
memo[X] = true;
X /= 2;
K--;
if (K < 0) return ans;
while (1 <= X) {
if (K == 0) {
ans++;
break;
}
memo[X] = true;
if ((2*X) !in memo) {
ans += count(2*X, K-1);
memo[2*X] = true;
}
if ((2*X+1) !in memo) {
ans += count(2*X+1, K-1);
memo[2*X+1] = true;
}
X /= 2;
K--;
}
return ans;
}
void read(T...)(string S, ref T args) {
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
これがACをとったコードですが、どのように動くかを具体的に見てみようと思います。
1
2 3
4 5 6 7
8 9 10 11 12 13 14 15
バックスラッシュが円マークになってしまうのでpreに位置関係を書きました。
一例として、X=6の動作を示します。
以下、countは指定した頂点を根とする部分木に対して答えを返す関数になります。
countにX=6とKを渡します。X=6をメモっておき、X/=2、K--とします(一つ上の階に上がる)2Xと2X+1のうち、メモに入っていない方、およびK-1をcountに渡します。また、Xもメモっておきます。- これを
1 <= Xである間(根にたどり着くまで)繰り返します。K=0になったりしたときには適切に処理します。
という感じです。これでもれなく探索できます。
計算量はcountが1回につきO(log(N))程度で、Xから1になるまで上に登っていくので、大体クエリ1回あたりO(log^2(N))くらいです。多分。
最初の実装では、countに渡した2Xまたは2X+1のノードが存在しない時にバグっていたようで、なかなか気づかなくて大変でした。
最後何とか気づいてギリギリ通りました。
おそらくもっと良い解法があるので、復習します。
F以降はほぼ見てないです。
感想
Eが解けてよかったー
これからもできる範囲で精進頑張ります。