ABC315参加記録
Published on 2023-08-24Last Modified 2023-12-01
Table Of Contents
はじめに
本稿は2023/8/19に行われた ABC315 の参加記録です。
戦績
今回の提出は以下のとおりです。
レーティング変化は以下のとおりです。
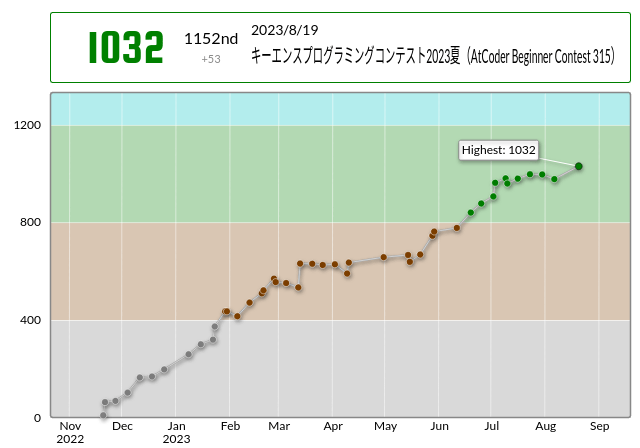
A, B, C, D, Eの5完で、レーティング変動は 979=>1032(+53)でした。
所感
今回でついにレーティング1000の大台に乗ることができました!かなり嬉しいです。 最近のABCでかなり手痛い負け(負けでないにしろ、解けないとダメだった問題を落としたり)が続いていたため、 今回で多少モチベが回復したような気がします。
コンテストに対する感想としては、今回D問題がかなり重実装(?)の問題だったようです。 当たりの方針を引いて、かつうまく実装できないと解くのが難しかったようで、difficultyが水色になっていました。 私は運良く筋の良い方針を見つけることができたため、なんとか通すことができました。 これが今回のパフォーマンスの上ブレに繋がったようです。
E問題は解けはしましたが、割と試行錯誤して通した感じがあります。 もっと問題の本質を見極められるようになりたいなと思います。
解法
A - tcdr

Sの長さが十分に短いので、一つづつチェックするだけで良いです。 一文字のチェックに5回の同値判定をすれば良いので一回の判定がO(1)、全体O(|S|)です。
B - The Middle Day

制約から、必ず真ん中の日が存在して、それは(Dの総和+1)/2になります。
D_1から順に総和をとっていき、初めて(真ん中の日)<=(総和+D_x)となるxが真ん中の日を含む月になります。
また、その月の(真ん中の日)-(総和)日目が真ん中の日になります。
混乱してしまう場合は、一旦紙に書いて一つづつ数えるとわかりやすいと思います。(自分もこういうの苦手です。)
計算量は、総和でO(M)、前からのシミュレーションでO(M)であるから、全体O(M)です。
C - Flavors

素直にやるなら、N個から2つ選ぶ全探索のO(N^2)です。 これは間に合いません。
この手のO(N^2)(だけではないが)が通らないタイプの問題にはいくつかパターンがあり、よくあるのは
- 何らかの前計算をしておき、各ケースの計算量を落とす。
- 分割統治で擬線形時間に落とす。(例: ソートなど)
- 動的計画法により前進的に(そうでない場合は、トポロジカル順に)求める。
- 実は探索するべきものはそんなに多くない。
とかです。 今回は、問題をよく見ると、全探索を減らすことができそうだとわかります。 場合分けしましょう。
- 2つのアイスの種類が同じ: 美味しさのトップ2を取ればよい。
- 2つのアイスの種類が違う: (異なるアイスの)美味しさのトップ2を取れば良い。
さて、1番はO(N)個の候補しかなく、2番は高々一つの候補しかありません。 ただし注意として、これらのうちどちらか片方は候補が一つも存在しないことがありえます。(両方候補がなくなることはないです。)
前処理をさくっとできれば、残りは線形時間で処理できそうです。
というわけで、アイスを種類ごとに振り分けてソートし、(存在すれば)それぞれの候補値のmaxを取れば良いです。
私は候補が存在しないケースに気づかずに2WAしました:(
D - Magical Cookies

今回の激ヤバ問題です。 色々考えました。
最初は印をつけたやつを即時消してよいのかと思っていました。 しかし、サンプル2を見て、定義された操作の順番に操作しないとダメなケースがあるなと気づき、 シミュレーションで解く方向に舵を切りました。
完全にそのままシミュレーションしてしまうと、 一回の操作あたりO(HW)となり、全体O((HW)^2)になりそうだなーという感じでダメそうです。 というわけで、配列で各行、各列の「残っている色の種類数」「クッキーの総数」を管理しながらシミュレーションしました。
削除する列(行)となくなるクッキーの色をキューで管理して、楽に削除クエリを処理できるようにしました。(説明が難しい)
自分の文章力だと限界なので、提出例から読み取ってくれ(丸投げ)
E - Prerequisites

順番を考えなければ、必要な本を見つけるのはそれほど難しいことではないです。 具体的には、「その本が必要とする本」へ辺を張って、本1から辿れる連結成分が必要な本です。 無向グラフにしてしまうと変な本を取り込んでしまうおそれがあるので、有向グラフでやりましょう。
変な本を取り込む例: 本1が本2を必要とし、本3が本2を必要とするとき、連結成分に本3も含まれるが、別にいらない。
この連結成分をいい感じの順番で出力すればACです。 ある時点で読むことのできる本の条件は、その本が必要とする本を全部読んでいることです。 これをグラフで表現すると、その本から有向辺でつながっている本を全部読み終わっていることといえます。
ここで、出次数をうまく扱います。 先程の条件は、出次数を用いると、「出自数が0の本なら読んでも良い」になります。 読んだ本へと伸びている辺を切っていけば(辺の始点の出次数を減らせば)順番に上がっていくことができます。
すまん、うまく説明できない。「トポロジカル順序」でググってくれ(丸投げ)(最悪)
自分の提出では、有向辺を逆向きにたどるために、後から逆方向の辺を張って無向グラフに変えています。
終わりに
ブログエントリ作るの時間かかる上に、問題をちゃんと解けないとネタがないから割と大変です。。 このブログはかなりメチャクチャな構造をしているので、最近どうにか改装しようと頑張っているのですが、こっちも思った以上に大変で心が折れそう。
まあなんにせよ引き続き競プロがんばります。