ABC310参加記録
Published on 2023-07-17Last Modified 2023-12-01
Table Of Contents
はじめに
本稿は、2023/7/15に開催された ABC310 の参加記録となっています。
戦績
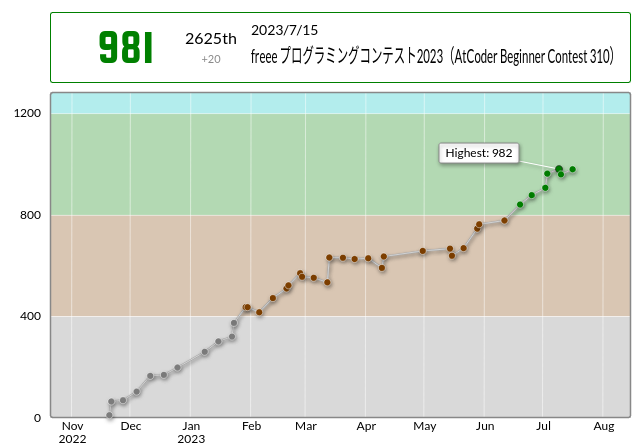
まずは、今回の戦績です。 A,B,Cの3完で、パフォーマンスは1142で、 レーティング変化は961=>981(+20)でした。
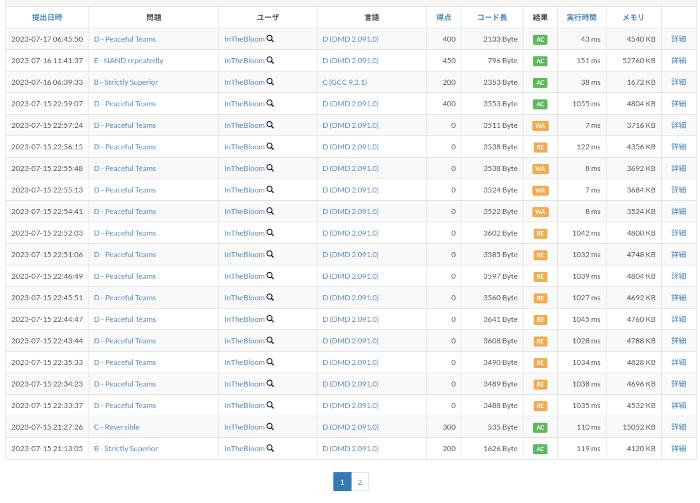
今回の提出は以下の通りです。
所感
今回久しぶりに本番中にD問題が通せませんでした。 かなり悔しいとともに、何故かパフォーマンス1000以上が出て割とレートがプラスになったのは少し腑に落ちない感じです。
後で発覚したのですが、実はD問題は解けていて、配列の範囲外参照によるREで落ちていたようです。(上の提出記録にあるように、どこでRE引いてるのかわからなくて提出でバッグを試みていました。)
というのも、実はD言語はAtCoder側でコンパイルオプションがリリースモードになっているようで、配列の範囲外参照を拾ってくれないんですよね。
なので、try-catchでエラーを捕まえてデバッグしようとしても無駄でした。
これマジでどうにかしてほしいんですが...
更にいうとE問題も正直ムズいと思います。 適当にDPもどきみたいなものを書いて通したんですが、解説が難解でよくわからなかった(小並感)
こういうのを適当な理解で済ませると後で痛い目を見ると思うので、ちゃんとなんで解けてるのか究明しないといけないわけです。 しかし、より広い問題設定に耐えうるような包括的な理解というものは難しいものですよね。(諦観)
問題と解法
解けた問題について振り返ろうと思います。 今回試験的に問題文を丸コピしてみます。特にことわりがなければ、問題名のリンク先が引用元になっています。
A - Order Something Else
問題文
高橋君は、レストランで「AtCoder ドリンク」というドリンクを飲もうとしています。 AtCoder ドリンクは定価である $P$円を払えば飲むことができます。
また、高橋君は割引券を持っており、それを使うと AtCoder ドリンクを定価より安い価格である $Q$ 円で飲むことができますが、 その場合には AtCoder ドリンクの他に、$N$ 品ある料理の中から 1 つを追加で注文しなければなりません。$i=1,2,…,N$ について、$i$ 番目の料理の価格は $D_i$ 円です。
高橋君がドリンクを飲むため支払う合計金額の最小値を出力してください。
解法
仮に他に料理を頼むなら、一品だけ頼むのが最適になります。 したがって、料理を頼まないときの金額と、一品だけ料理を頼むときの金額を全部見て、それらの最小値が解になります。 制約も十分小さいのでこれでACできます。
B - Strictly Superior
問題文
AtCoder 商店には $N$ 個の商品があります。 $i$ $(1\leqq{}i\leqq{}N)$ 番目の商品の価格は $P_i$ です。 $i$ $(1\leqq{}i\leqq{}N)$ 番目の商品は $C_i$ 個の機能をもち、$i$ $(1\leqq{}i\leqq{}N)$ 番目の商品の $j$ $(1\leqq{}j\leqq{}C_i)$ 番目の機能は $1$ 以上 $M$ 以下の整数 $F_{i,j}$ として表されます。
高橋くんは、AtCoder
商店の商品で一方が一方の上位互換であるものがないか気になりました。 $i$
番目の商品と $j$ 番目の商品 $(1\leqq{}i,j\leqq{}N)$
であって、次の条件をすべて満たすものがあるとき Yes と、ないとき No
と出力してください。
- $P_i\geqq{}P_j$ である。
- $j$ 番目の製品は$i$ 番目の製品がもつ機能をすべてもつ。
- $P_i>P_j$ であるか、$j$ 番目の製品は $i$ 番目の製品にない機能を $1$ つ以上もつ。
解法
問題が結構ワチャワチャしていて読解が大変ですが、やること自体はシンプルです。 しっかり読み取るべき情報は、
- 各商品の「機能」は、1以上M以下の値からなる100項以下の数列で表される(以後、「機能数列」と呼ぶ)
- 「商品iと商品jが機能xを持つ」とは、どちらの商品の機能数列もxを含むことである
ということです。
これを踏まえた上で、「商品iが商品jの上位互換である」ということを次のどちらかの条件を満たすことと定めます。
- すべての商品iの持つ機能を商品jが持ち、逆に、すべての商品jの持つ機能を商品iが持つ。 かつ、商品iの値段が商品jの値段未満である
- すべての商品jの持つ機能を商品iが持ち、かつ、ある機能が存在して、商品iはその機能を持ち、商品jはその機能を持たない。 かつ、商品iの値段が商品jの値段以下である。
堅苦しく書いたのはそっちのほうが実装に落とし込みやすいかなと思っているからです。 これを正確に実装すればACが取れます。 なお、機能を持っているかのチェックは二重ループなどによる全探索でも余裕で間に合います。
C - Reversible
問題文
ボールがいくつか刺さった棒が N 本あり、各ボールには英小文字が $1$ 個書かれています。
$i=1,2,\cdots{},N$ について、$i$ 番目の棒に刺さった各ボールの英小文字は、文字列 $S_i$ によって表されます。 具体的には、$i$ 番目の棒には文字列 $S_i$ の長さ $|S_i|$ に等しい個数のボールが刺さっており、 刺さっているボールの英小文字を、棒のある端から順に並べたものは文字列 $S_i$ と等しいです。
$2$ つの棒は、一方の棒に刺さっているボールの英小文字をどちらかの端から並べた列と、もう一方の棒に刺さっているボールの英小文字をどちらかの端から並べた列が一致するとき、同じ棒とみなされます。 より形式的には、$1$ 以上 $N$ 以下の整数 $i,j$ について、$i$ 本目の棒と $j$ 本目の棒は、$S_i$ が $S_j$ と一致するか、$S_i$ が $S_j$ を前後反転したものと一致するとき、かつそのときに限り、同じとみなされます。
$N$ 本の棒の中に、何種類の異なる棒があるかを出力してください。
解法
ややこしいですが、言ってることはこうです。2つの文字列a, bが等しいということを次で定める。
- aとbが等しい
- aを逆順にしたものとbが等しい
いくつか文字列が与えられます。相異なる文字列はいくつありますか?
素直に全探索するとO(N^2)で間に合いません。 そこで、連想配列などを利用します。
解法1: 全部の回分でない文字列と、全部の回分でない文字列の逆順を連想配列に登録して、登録数を2で割ったものと回分の和を取る。
解法2: 全部の文字列を登録する。 その後、それぞれ回分でないものを逆順にしたものが連想配列に登録されているかを見ていき、 登録されていたら、逆順にする前の文字列を連想配列から除去する。 最後に登録数を出力。
解法1はほぼ自明です。解法2は、これを行うことでもとの文字列を逆にしたものだけが残ります。 ある文字列と、その逆順文字列がどちらも与えられるパターンと、そうでないパターンについて考えると証明できそう(知らん) 回文が色々とコーナーケースになっているので気をつける必要がありますが、サンプルに載っています。
自分はアホなので解法2を取りましたが、普通に考えて解法1のほうが楽です。
D - Peaceful Teams
問題文
$N$ 人のスポーツ選手がいます。
$N$ 人の選手たちには互いに相性の悪い選手のペアが $M$ 組あり、相性の悪い組のうち $i$ $(1\leqq{}i\leqq{}M)$ 組目は $A_i$ 番目の選手と $B_i$ 番目の選手です。
あなたは、選手を $T$ チームに分けます。 どの選手もちょうど一つのチームに属さなければならず、どのチームにも少なくとも一人の選手が属さなければなりません。 さらに、どの $i=1,2,…,M$ についても、 $A_i$ 番目の選手と $B_i$ 番目の選手が同じチームに属していてはいけません。
この条件を満たすチーム分けの方法は何通りあるか求めてください。 ただし、チーム分けの方法が異なるとは、ある二人が存在して、彼らが一方のチーム分けでは同じチームに所属し、もう一方では異なるチームに所属することをいいます。
解法
私は公式解法2通りのどちらでもない解法で無理やり通したので、それを書きます。 まず、少なくとも一人がチームにいないといけないということなので、nCtを全列挙します。
nCtで選ばれたT人を、前からチーム0,1,2,...,T-1に割り当て、 残ったN-T人をN-TビットT進数と見てビット全探索します。 ビットがiの人をチームiに割り当てることにすると、 すべてのチームの分け方を探索できます。
しかしこのままだと、チームの分け方が重複する場合が存在します。 重複の数はチームiのメンバー数を$m_i$とすれば、$\displaystyle\prod_{i=0}^{T-1} m_i$となります。 よって、重複数で分けて総和を取り、最後に重複数で割った総和が答えになります。
最初にnCtをしているのはビット全探索パートの計算量を落とすためです。 計算量は全体で$O(N*({}_n\mathrm{C}_t)*(N-T)^T*(チーム分けがOKかどうかの一回の判定分))$くらいかなぁ...よくわからん。
細部を説明するのは大変な上、かなり怪しい解き方なのでこれ以上は言及しません。
余談ですが、公式解説の全探索とdpはもっと一般化した主張にできるんじゃないかな(できたら便利そうだな)と思っていますが、 数学無理なので無理です。(は?)
E - NAND repeatedly
問題文
0 と 1 からなる長さ $N$ の文字列 $S$ が与えられます。 $S$
は長さ $N$ の数列 $A=(A_1,A_2,…,A_N)$ の情報を表しており、$S$ の
$i$ 文字目 $(1\leqq{}i\leqq{}N)$ が $0$ のとき $A_i=0$ 、$1$
のとき $A_i=1$です。
$$ \sum_{1\leqq{}i\leqq{}j\leqq{}N} (\cdots{}((A_i\bar{\land{}}A_{i+1})\bar{\land{}}A_{i+2})\bar{\land{}}\cdots{}\bar{\land{}}A_j) $$
を求めてください。
より厳密には、次のように定められる $f(i,j) (1\leqq{}i\leqq{}j\leqq{}N)$ に対して $\displaystyle\sum_{i=1}^N \displaystyle\sum_{j=i}^N f(i,j)$ を求めてください。
$$ \begin{equation*} f(i,j)= \begin{cases} A_i & \text{$(i=j)$} \\ f(i,j−1)\bar{\land{}}A_j & \text{$(i<j)$} \end{cases} \end{equation*} $$
ただし、否定論理積
$\bar{\land{}}$ は次を満たす二項演算子です。
$0\bar{\land{}}0=1,0\bar{\land{}}1=1,1\bar{\land{}}0=1,1\bar{\land{}}1=0$
解法
普通にやるとO(N^2)で間に合いません。そこで、何かしらの性質を利用する必要がありそうだとわかります。 演算が左結合であり、演算の結果取りうる値が0か1しかないということを利用して計算します。
$dp[i][j]:=$(左からi文字目まで見て、値がjであるような場合の数)
としてやるとうまく行きます。 $\displaystyle\sum_{i=0}^{N-1} dp[i][1]$が答えになります。
正直よくわかっていませんが、始点を固定したとき同じ領域を何回も計算しているのを圧縮しているっぽいです(適当)
この辺もちゃんと解けるようになりたいなぁ
終わりに
今週のABCは色々とだめなところが多かったなと反省です。 ここ最近精進をちょっとサボってしまっていたのが悔やまれるので、今週はしっかり取り組みたいです。
今回出題された問題は最近の中でも特に学びが多そうな雰囲気があるので、復習もがんばります。
あと、問題文コピってくるのラクかなーって思ってやってみましたが、クソ大変でした。二度とやりません。