ABC307参加記録

はじめに

本稿は、2023年6月24日に行われたABC307の参加記録です。

戦績

今回の戦績です。 今回はパフォーマンス1166で、 レート変動は842->879でした。

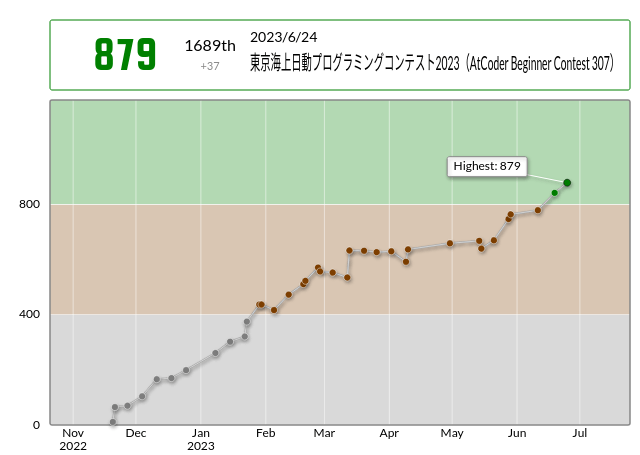
コンテスト中にA,B,C,Dの4完することができました。 また、コンテスト後にE問題を通すことができました。

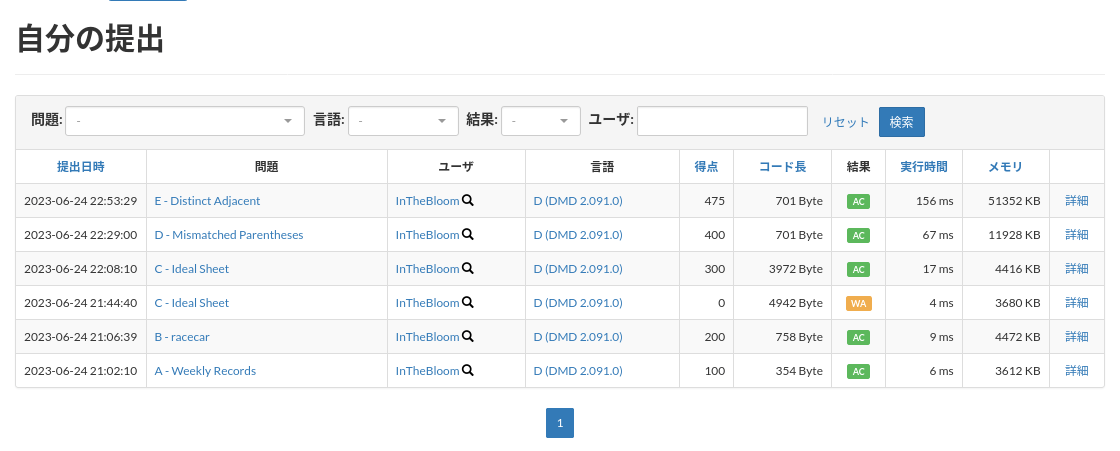
解いた問題

A - Weekly Records

問題文に書いてあることをそのまま行います。$A_i$があまり大きくないので普通にintでOKです。 私は前から足していって、7の倍数番目の番号のとき出力とリセットをしました。 ただし、通常プログラミング言語では0-indexedなので、i+1を考える必要があります。 (詳細は提出コードを参照)

提出

B - racecar

$N$が十分に小さいので、すべての$i$,$j$について$S_i$と$S_j$の連結が回文になるかどうかをチェックする方法でOKです。 二重ループなどで解くと良いでしょう。

C言語で解くなら、不定長の文字列を受け取るテクニックが使えます。 まず、charの配列を$51*N$程度で宣言します。 その後、char*の配列を$N$要素で宣言して、 各char*の$i$番目の要素が$S_i$の先頭を指すようにすると省メモリで扱えます。 具体的には次のようにします。

#include <stdio.h>

int main (void) {
    int N; scanf("%d", &N);

    char SS[51*N];
    char *S[N];
    int len[N];

    int idx = 0;
    for (int i = 0; i < N; i++) {
        char tmp[51]; scanf("%s", tmp);
        int j = 0;
        S[i] = &SS[idx];
        for (; tmp[j] != '\0'; j++) {
            SS[idx++] = tmp[j];
        }
        len[i] = j;
        SS[idx++] = '\0';
    }
}

うーん、C言語辛い！w

提出(C言語ではないです。)

C - Ideal Sheet

今回の激ヤバ問題です。 C問題なのにdifficultyが1200を超えています。(結構な人がスルーしたみたいです。)

要は、いい感じに文字列を組み合わせて、与えられた模様を作れるか？という問題です。 結構激重実装問題っていう風に言われていますが、 私はむしろ、どうやって解くか？という部分が一番大事になるんじゃないかと思いました。 というのも、シートAとシートBを張り合わせる土台を適当に超巨大に作ってしまうと 計算量がエラいことになってしまうからです。

私の方針としては、概ね次のような感じです。

• シートA, B, Xの透明部分を長方形であることだけを保ったまま可能な限りカット
• 土台としてX(をカットしたもの)と同じサイズのものを用意する
• シートA, Bをはみ出さないように貼り付ける手順を全探索
• 土台とXが一致しているかチェック

というような感じで解きました。 ポイントが、土台をXのカットと同じサイズにすることです。 明らかにこれが土台の限界の小ささになります。 マージンを取りすぎると全探索が多くなりすぎてTLEするみたいです。

というわけで気合でACできました。 こういう「カットできるとこをカットする」みたいな操作は絶対にC言語で実装したくないです。(強い意思)

提出

D - Mismatched Parentheses

文字列から「有効な括弧列」を削除する問題です。 有効な括弧列を処理するのにはスタックが非常に向いています。 というのも、その定義の一つに

「連続する()を削除することを0回以上繰り返して空文字列にできるもの」

というものがあるので、 明らかに)を見つけたら(までスタックから取り除く という方法で有効な括弧列を除去することができてしまいます。

後は現在スタックの中に(が何個あるかという情報を持っておくと、 )からスタックを削っていって(が見つかるかどうかを判定することができ、 残すべきところと残すべきでないところを判断することができます。

ただ、私は(の個数を管理するということまで思い至らなかったため、 「たどっていってる途中で(が見つかる前にスタックが空になってしまったらansに追加する」 という感じで解きました。計算量はO(N)です。

提出

E - Distinct Adjacet

見た目がなんかいかつそうな問題です。 まず、問題を単純化してみます。 例えば、輪っかになっていないという仮定をしてみます。

左から一人ずつ決めていくとして、 受け取ってはいけない数字は一つ左の人のみに依存するので、最初の人がM通り、 次の人からは全員M-1通りになり、答えは$M*(M-1)^{N-1}$になりそうです。

フムフム、結構自由度が高いんだなと考えながら、 輪っかの方の考察に戻ってみます。

輪っかの方もほとんど同じで、最後の一人以外は一つ左の人のみに依存するので、$M-1$通りになりそうです。 最後の一人は、最初の一人にも依存するので、状況が少し複雑になります。

• 最初の一人と最後から二番目の人が同じ数字のとき

このとき、明らかに$M-1$通りになります。

• 最初の一人と最後から二番目の人が違う数字のとき

このときは$M-2$通りです。

最後から二番目の人が最初の人と同じ数字である場合の数を考えるには、 最後から三番目の人が最初の人と同じ数字かどうかを知る必要があります。 アレ、ややこしくなってきましたね。

それならいっそ「$i$番目の人が、最初の人と同じ数である場合の数」と、 「最初の人と違う数である場合の数」を考えればよいのではないでしょうか？

これなら順々に計算できそうです。 というわけで、DPします。

$dp[i][j] := i人目が状態jであるような場合の数$

とします。ここで、$j=0$は一人目と同じ数字、$j=1$は一人目と違う数字であるとします。 初期値は、 $dp[0][0] = M$, $dp[0][1] = 0$となります。

漸化式は

$dp[i][0] = dp[i-1][1]$

$dp[i][1] = (M-1) * dp[i-1][0] + (M-2) * dp[i-1][1]$

となります。 これをあまりを取りながら計算して、$dp[N-1][1]$が解になります。

DP難しいよ〜

提出

終わりに

最近緑になれましたーヤッター

競技プログラミング死ぬほど難しいけどなんとかがんばります。

あと、ICPC出れそうです。そっちの方も適当にがんばります。