ABC304参加記録

Published on 2023-06-05
Last Modified 2023-12-01

はじめに

競技プログラミングに対してやる気がわかない夜は、コンテストの参加記録を書こう。 そうしよう。

というわけで、ABC304の参加記録です。

戦績

残念ながらジャッジにトラブルがあったようで、今回のコンテストはunratedになってしまいました。 そのため特にレート変動はありません。

今回の提出結果はこちらです。

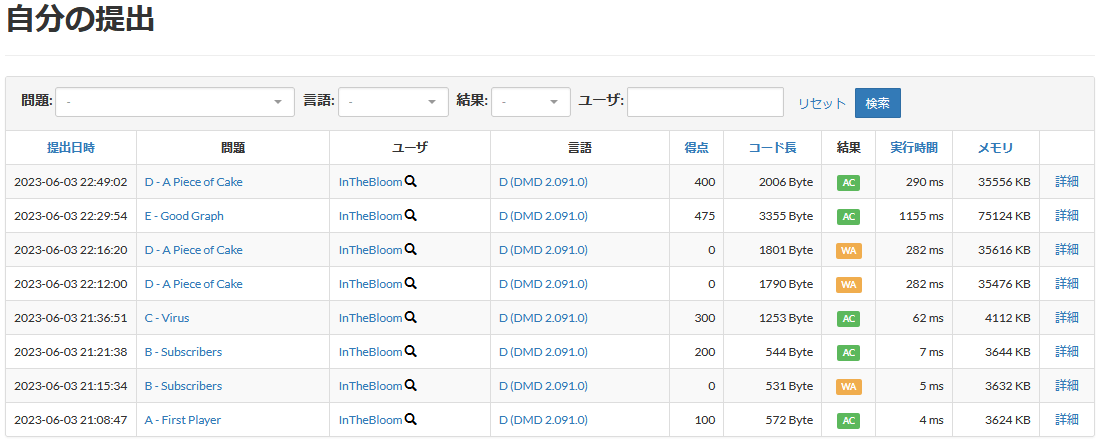
AからEまでの5問正解することができ、全部で3ペナルティ食らいました。

問題と解法

コンテスト中にACできた問題についてかるーく振り返ります。

A - First Player

A問題です。難しかった…

やること自体は簡単(に理解できるもの)ですが、この問題プログラミング始めたばっかりの人結構大変なんじゃないんですかねとか思いました。 この問題は剰余演算を用いることで簡単に解くことができます。 具体的にはx番目に最年少の人が来たとするとき、0<=i<=N-1であるiを用いて(x+i)%N番目の人の名前を出力することでACできます。

要はインデックスの余りをとってあげることでちょうどテーブルを一周できるわけです。 これよりもシンプルで初心者向けの解法が思いつきません。

提出

B - Subscribers

見た目がヤバいですね。ちなみに実際ヤバいです。 私の脳裏にこれが思い浮かびました。

「切り捨てる」という操作を、「元の数から、元の数を10^x^で割った余りを引く」という操作に置き換えます。 これを頑張ってifやswitchなどで場合分けするとACできます。 途中で混乱しないようにしましょう(1敗)

これWA出たとき台パンしそうになった()

あと関係ないですが、この問題名が「Subscribers」になっているのはYoutubeの登録者数表示に準拠してるのかな？とか思ったり(知らんけど)

提出

C - Virus

これもなかなか難しい！ AtCoder Problems上で確認したところ、difficultyは366らしいです。

まず、制約を見ます。 割と制約がゆるそうなので、雑な全探索が通りそうな気がします。

ある感染者から感染する人を探したいとき、自分自身以外のN-1人を1回ずつ見れば十分なことが分かります。 また、探索の基準にする感染者をいちいち記録しておかなければいけません。 そこで、キューを使ったアルゴリズムを考えました。

1. キューに人1を入れる。
2. キューから人を取り出し、その人に対して、「調べ済み」の印をつける。
3. 「調べ済み」のしるしがついていない人で、キューから出した人との距離がD以下の人を見つけたらその人に「調べ済み」の印をつけてキューに入れる。
4. キューが空でなければ手順2に戻る。空なら手順5に進む
5. すべての人について、「調べ済み」の人はYes、そうでない人はNoを出力する。

よくよく見るとこれは「距離がD以下の人同士で無向辺をつないだグラフのBFS」とみなせます。 解いてるとき全く気付かなかった。。。 グラフとして見れたらもっと早く処理できたかもしれないなぁと思います。

提出

D - A Piece of Cake

これ、難しくないですか？？？ 私は結構苦戦しました。

まず、制約を見た感じ長方形領域を一つ一つ見ていく方法は絶対に不可能なことが分かります。 ということで、「同じ領域に存在するイチゴならば同じ情報になる」というような情報の圧縮を考える必要があります。 逆に言うとイチゴの数はそこまで多くないわけですから、そのような圧縮が存在すれば簡単に解けるということです。

結論から言うと、「ケーキを切り分ける直線のインデックス」を用いるとうまくいきます。 例えば、一つのイチゴに対して順序対(X, Y)を以下のように定義します。

X := (イチゴのx座標よりも小さい最小のaのインデックス)

Y := (イチゴのy座標よりも小さい最小のbのインデックス)

一つ注意として、制約が0 < a, bなのでa, bの配列の先頭に0を追加しないと上の定義ができません。 私は0を追加して解きました。

このようにすると、同じ領域に存在するイチゴは同じ順序対が割り当てられます。 あとはこれらを連想配列などで管理します。

mを求めるときにも少し注意する必要があります。 上の方法では切り分けた領域をすべて見ているわけではないので、一つもイチゴが乗っていない領域が存在するかどうかが分からないという問題があります。 これは、(連想配列の登録数)と(A+1)*(B+1)の大小関係で確定させることができます。 後者がより大きい時は必ずイチゴが乗っていない領域が存在します。 ということでACをとることができます。

提出

E - Good Graph

なんか奇跡的に解けた問題です。

「頂点x_iとy_iを結ぶパスが存在しない」という条件は、まさしくx_iとy_iが連結でないということを示しています。

そのような予想の元、クエリにどうこたえるかを考えてみます。 頂点p_iとq_iを結ぶことでよいグラフが崩れるかどうかを判定するということは、 p_iとq_iの所属する連結成分が分かれば判定可能です。 具体的に言うと、あるjに対して、p_iとx_jが同じ連結成分に属していて、かつq_iとy_jが同じ連結成分に属していたらだめですね。

グラフGのそれぞれの連結成分を、ある代表元を用いて管理することで上の判定問題を高速に解くことができます。 …はい、まんまUnion-Find Forestです。

具体的な解法としては以下のようになります。

1. グラフの連結成分を構築。
2. x_iとy_iの代表元を見つける。それをX, Yとして、(X, Y)と(Y, X)を連想配列などに追加しておく。
3. p_iとq_iの代表元を見つける。それをP, Qとして、(P, Q)が連想配列に登録されていたらNo、されていなければYesを出力する。

このようにしてACできます。

最近Union-Findもといdsuを用意したので、ドンピシャで使いどころが来てくれてなかなかうれしいです。 ただ、私のUnion-Findやたら動作が遅いのですごく心配です。 経路圧縮とUnion by sizeやってるはずなんだけどなぁ

提出

終わりに

最近D問題とかE問題が解けるときがあってうれしい！ 引き続き競技プログラミング(というかAtCoder)に取り組んでいきたいと思います！

ここまで読んでいただきありがとうございます。 それではまた次のエントリで。

---