ABC300参加記録
Published on 2023-05-01Last Modified 2023-12-01
Table Of Contents
ABC参加しました。
今回も ABC300 に参加してきました。 久しぶりに参加記録を書きます。
戦績
まずは、今回の戦績をざっくり振り返ります。 以下は今回の提出です。
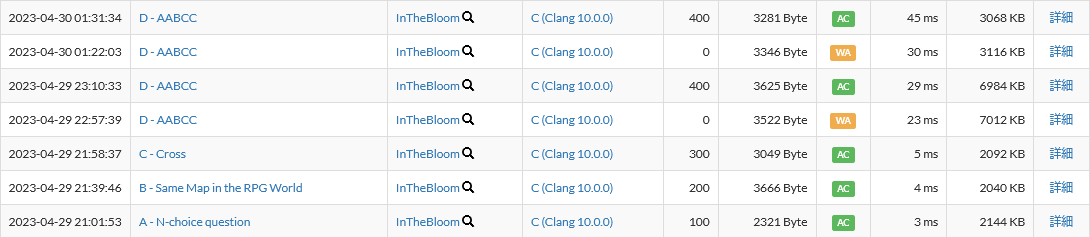
今回は時間内にA, B, Cの3問を解くことができました。 また、コンテスト後にD問題を解くことができました。 レート変動はこちらです。
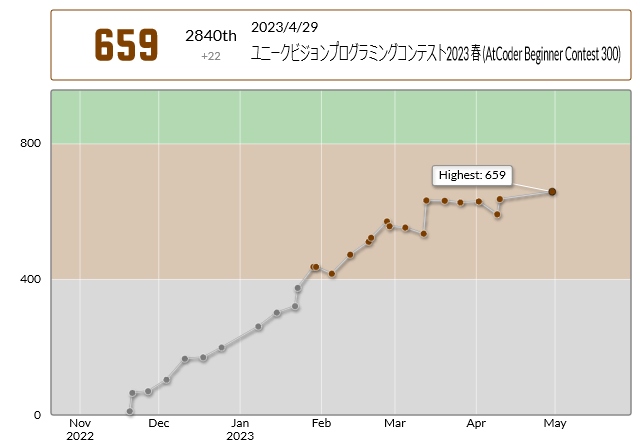
何とかプラスのレートを得ることができました。速く700行かせてくれー
問題と概要
今回解けた問題の軽い解説(?)をしていきます。ざっくりです。
A - N-choice question
問題文は以下の通りです。

問題文に書いてあることをその通りにやります。A+Bを変数に持っておいて、何番目のC[i]と一致するかを見つければよいです。
ループとstdinの扱いができればACできると思います。
提出例です。
#include <stdio.h>
int main (void) {
int N, A, B;
scanf("%d%d%d", &N, &A, &B);
for (int i = 0; i < N; i++) {
int tmp; scanf("%d", &tmp);
if (tmp == A + B) {
printf("%d\n", i + 1);
break;
}
}
return 0;
}
B - Same Map in the RPG World
問題文は以下の通りです。

この問題はB問題のわりにかなり難易度が高かったようで、 AtCoder Problems 上で400くらいのdiffがありました。 シンプルに言うと文字列の一致判定問題といえるでしょう。 ただし、片方の文字列に対して2つの操作を許されています。
- 列を一つずつ右にずらす。一番右の列は一番左にワープする。
- 行を一つずつ上にずらす。一番上の列は一番下にワープする。
サンプルが問題ページに乗っているので気になる人は見に行って見てください。 さて、この問題は十分に制約が緩いので、操作1, 2のすべての組み合わせを行うことができます。 具体的には、操作1をH回、操作2をW回行う2重ループをすることで正誤判定をすることができます。 典型テク「全探索ができるならやろう」です。
C - Cross
問題文は以下の通りです。

なかなかいかつい見た目ですね。 少し整理しましょう。 まず、問題文において「サイズnのバツ印」は(ざっくり)以下のように定義されています。
- あるマスが
#で、斜め4方向にn個の#が隙間なく続いている。 - 斜め4方向にn+1こ
#が続いてはいけない。(これを許すとサイズ1~nのバツ印とn+1のバツ印が被っちゃう)
サンプルです。
#...# .#.#. ..#.. .#.#. #...#
これはサイズ2のバツ印です。サイズ1のバツ印を含んでいますが、ルール2により却下されます。
.#...# ..#.#. ...#.. ..#.#. .#...# #.....
これは一辺だけサイズ3ですが、ルール1によりサイズ2と判定されます。
問題としては、(よくわからんけど)割と親切な文字列が与えられるので、「サイズ1~min(H, W)」のバツ印が何個あるか判定してくださいというものです。
解法としては、あるマスが#だった時にそこを中心としてバツ印がつくれるか?をすべてのマスに対して適用しました。
制約が比較的緩いので、上のルールでも十分動作します。
関数化したらこんな感じです。
int cross_size (int W, int H, int x, int y, char C[][W + 1]) {
for (int i = 1; ; i++) {
if (W - 1 < x + i || x - i < 0 || H - 1 < y + i || y - i < 0) {
return i - 1;
}
if (C[y + i][x + i] == '#' && C[y + i][x - i] == '#' && C[y - i][x + i] == '#' && C[y - i][x - i] == '#') {
} else {
return i - 1;
}
}
}
D - AABCC
問題文は以下の通りです。

出、出た~!数学問題奴~www
なんかNの制約が割と大きそうなので、単純な探索だと厳しいという予想を立てました。
手元のカードとして「エラトステネスの篩」というものがあったので、素数を探索するのは下準備さえあればできるということを考えながら思案。。。
典型テクニック「変数が一つ以外決定されているときを仮定」をやってみると、b以外を固定すればすぐに答えられそうというのがわかる。
また、aとcは大体10^3^~10^6^くらい探索すればよいので二重ループしても間に合いそうだな…という考えに至る。
求めたNが被ることは…素数だから多分ヨシッ!
したがって、以下のアルゴリズムを考えた。
- エラトステネスで大体10^6^くらいまで素数列挙
- a, cをa^2^+c^2^ < Nの範囲で探索、それぞれのケースに対してbをいい感じに数え上げる。
さて、具体的にどうやってやるべきだろうか。 例えばあるa, cに対してbのとりうる最大と最小を考えると、数直線上の閉区間の素数の数を即座に答える必要がある。 アッ!累積和使えるやん!
ということで、あとは実装したら完成。AC取れました。ただし、手順2のbをいい感じにっていうところがちょっと面倒くさいので、ここは丁寧に考える必要あり。
D問題はコンテスト中に間に合いませんでした。残念。 また、解説を見た感じ、素数の数があまり多くないからエラトステネスからのa, b, cの全探索で解けるそうです。
実際に、やってみた。
これは今の私には思いつかないですね。
E - Dice Product 3

何ともならんかったわ。(事後報告)
(画像は ここ から剽窃してきた。)
終わりに
まず、一か月くらい記事更新をさぼってしまって本当に申し訳ない。
なかなか記事更新にも時間がかかってしまうというのもありますが、できるだけ参加記録を公開したいな~(願望)
私事ですが、Bootcamp For Beginnersのmediumが終わりました。
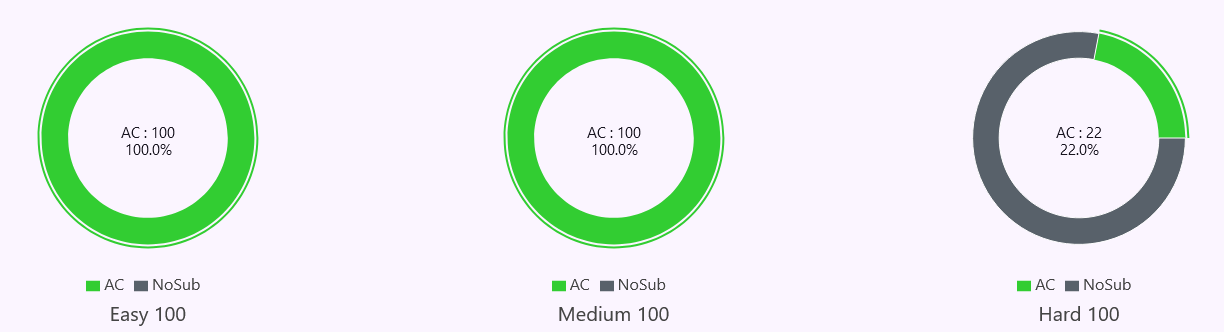
あと、longest streakが100日超えてました。

これからも頑張ります。
それではまた次のエントリで。