ABC296参加記録
Published on 2023-04-03Last Modified 2023-12-01
Table Of Contents
ABC参加してきました。
こんにちは。今回の ABC296 も参加してきましたので、軽い参加記録です。
戦績
今回の戦績についてです。
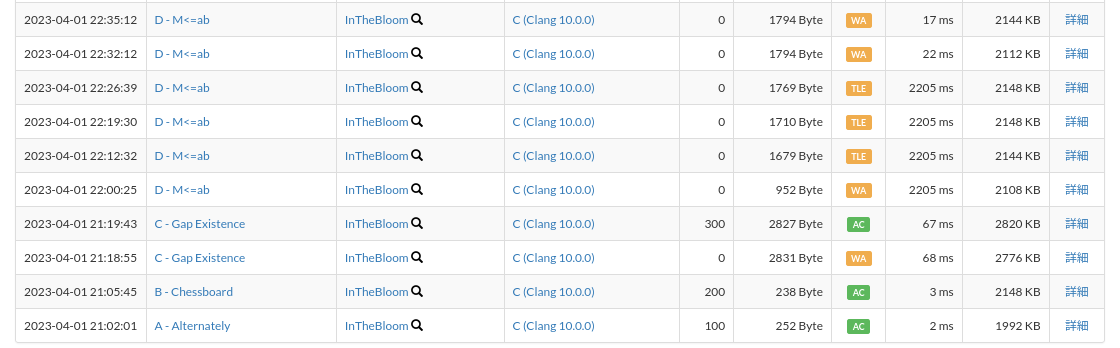
今回はA, B, Cの3完、パフォーマンス650で、レート変動は627→630(+3)でした。
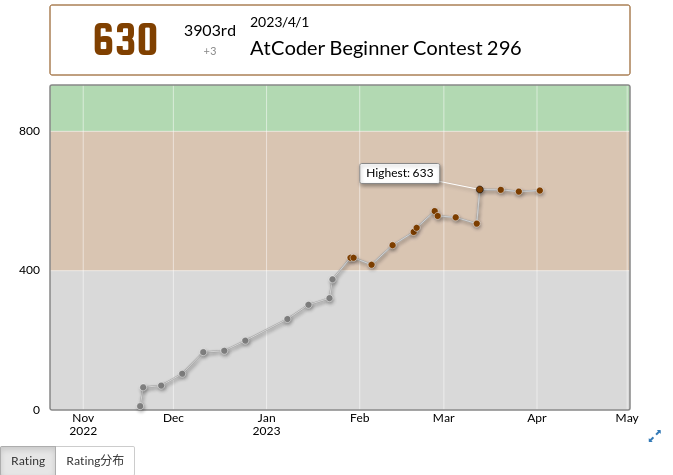
ギリ勝ちでした。
問題と解法
A~Dの4問の解法を紹介します。
A - Alternately
問題分は以下のとおりです。

男性または女性同士が隣り合っているかどうかを判定する問題です。シンプルに解くなら、文字列長をNとして、1文字目からN-1文字目までのそれぞれに対して以下の判定を行います。
i文字目とi+1文字目が一致しているか?
- YES→
Noを出力し、プログラムを終了 - NO→何もしない
この判定をN-1文字目まで行い、それでもプログラムが終了していなければYesを出力しプログラムを終了することで正しく判定することができます。
ほぼ自明な操作なので、文字列操作が適切に行えるならACが取れると思います。
B - Chessboard
問題分は以下のとおりです。

チェス盤の状態が文字列として渡されるので、コマが存在するマスを適切なフォーマットで出力する問題です。
制約から、コマが一つしかないことがわかるので、いわゆるオンラインアルゴリズムにて解くこともできます。
解法としては、文字列を一つづつ見ていき、*が存在する行番号と列番号を適切に変換すればよいです。注意点として、行数を表す番号は一番下が1番になっているため、出力するときには8-○のような形にする必要があります。
C - Gap Existence
問題分は以下のとおりです。

任意のi,
jを全探索することで解を得ることができますが、この解法では解が存在しなかったときにおよそ10^10程度の探索が必要になります。したがって、この方針ではACを取ることは現実的ではないです。
そこで、次のように問題を言い換えます。「あるA_iに対して条件を満たすA_jが存在するなら、A_j=A_i+Xを満たす。」
つまり、「与えられた配列の中に値がA_i+Xと等しいものはあるか?」という問題に変わります。
事前に配列をソートしておくことで配列の中から値を探すという典型問題に落とし込めます。この時、全体の計算量はO(Nlog(N))で抑えることができます。定数倍を考えなければ約10^6回程度の探索で解を得ることができます。
二分探索を自分で実装する場合、この問題のようにキーが配列中に存在しないことも考慮したコードを作成しておくと良いと思います。
D - M<=ab
問題分は以下のとおりです。

かなりシンプルな問題です。こういうの苦手です。
まずは私が試していたダメな解法を紹介します。
制約から、N*N>=Mならば、-1ではない何かしらの解が存在します。なぜなら、N*Nが解の候補の一つだからです。
そこで、まずN*N<Mとなるようなケースはすべて-1を出力して終了。それ以外のケースについて考えることにします。
解となる可能性があるXに対して、両方がN以下となるような因数分解を見つける方針で考えます。まず、Xの範囲を絞ります。仮定から、M<=Xです。
色々考えた結果、Xの上界は「M以上になるもののうち最小の平方数」であることがわかりました。理由は単純で、この値を上界とする時明らかにN*N以下となり、少なくとも「その平方数」が解の候補になるからです。
以上より、M<=X<=(平方数)に対して、2つともN以下になるような因数が存在するかを判定する問題になりました。
ここからは単純に、「Xの平方数に一番近い整数」からX=1になる、または割り切れるまで「Xを」順番に試し割をすればよいです。こうすれば2数の差が一番小さくなるような因数分解ができます。
試し割りで見つかった因数が両方N以下ならXを出力して終了、そうでないならXを1増やして同じことをすれば良いです。
この解法は正しく動作しますが、 制限時間内に終わりませんでした。結果としては10ケースでTLEが出てしまい、コンテスト中に通せませんでした。
雑な計算量解析をすると、まず私の絞り込んだXの範囲が、最悪ケースのときに連続する平方数の差とほとんど同じになります。これは(a+1)^2 - a^2 = 2*a + 1程度です。制約から、aは最大で10^6程度までありえます。そして試し割りは最悪ケースのとき、つまりXが素数の時には√X回程度かかります。流石に素数が密集しているとは思えませんが、平均的に見て√Xの定数倍程度になっているだろうと予想できます。これも10^6程度までありえます。以上より、最悪ケースのときには十分10^8回程度を超える計算が行われる可能性があります。
さて、この問題を解くためには別のアプローチが必要になります。
まず、重要な事実は次の2つです。
- 解となる可能性のあるX=abに対して、a<=bを仮定すれば因数aの上界は10^6である。
- あるaを一つ定めると、解となる可能性のあるbはただ一つ存在する。
それぞれについて検討していきます。まず1つ目です。制約より、M<=10^12となりますから、Xの因数a,bがどちらも10^6であれば、それは必ず解の候補になります。また、a,bどちらも10^6を超えるようなケースは存在しません。a=b=10^6がより優れた解の候補だからです。
2つ目に対しては、あるaに対して、a*bがMを超えるようなbのとり方は無数に存在しますが、解となり得るのはそれらのうち最小のものだけです。つまり、一つのaに対して必ず条件を満たしうるbが一つだけ存在します。
以上より、以下のアルゴリズムにてO(1)で解くことができます(10^6程度で抑えられるという意味です。)。
- 最初、a=1とする。解はans=-1としておく
- a*bがM以上になるような最小のbを求める。具体的にはM%a=0の時b=M/aで、それ以外のときb=M/a+1となる。
- a>bとなっていたらansを出力し、プログラムを終了する。
- b<=Nならばans=min(a*b, ans)とする。
- aを1増やし、2に戻る
私の解法が、「Xの取りうる値に対して、条件を満たすように因数分解できるか?」だったのに対して、こちらの解法は「解になり得る因数を全探索する」というような解法になっています。Xを構成的に見つけていくことで、各aに対して数回の演算でbを求めているのが高速化に寄与している点だと思いました。
この問題から学べる教訓としては、
- 復数の変数が出現する問題では、ある一つ以外の変数が事前に定まっているという仮定のもとでなにか得られないか考えてみる。
- できるだけ天下り的ではなく構成的に考える。
- 暗に大小関係を定めてしまえば探索範囲の重複を防ぐことができる(ことがある)
と言ったところでしょうか?次出会ったら解けるようになりたいですね。
終わりに
今回の参加記録はここまでです。読んでいただきありがとうございます。
最近4完がほぼできておらず、大体茶色MAXdiffあたりから解けるかどうか怪しくなっているような感じです。早いところそのあたりの難易度帯の対策もしたいですね。
サラッと先週分サボってごめんなさい。やる気があったらD問題だけでも記事書きます。
あと、現在私のC言語ライブラリのサイトをgithubで構築中です。近いうちに宣伝するかも?(宣伝の宣伝)
ではまた次の記事で