ABC294参加記録
Published on 2023-03-21Last Modified 2023-12-01
Table Of Contents
ABC294に参加しました。
こんにちは。今週も ABC294 に参加してきましたので,その参加記録です。
戦績など
まずは,今回の戦績です。

A, B, C, Dの4完でした。今回のパフォーマンスは626で,レート変動は633→632(-1)でした。
実は今回コンテスト開始に少し遅れてしまいました。それも相まって少しパフォーマンスが下がってしまいました。今回のE問題が普段に比べて簡単だったので5完チャンスだったのですが,少し間に合いませんでした。
問題の紹介
今回はコンテスト後にACをとることができたE問題まで紹介します。
A - Filter
問題文はこちらです。
この問題は,標準入力を適切に扱えるならすぐに解くことができます。制約も特に厳しい部分がないので,単純に一つずつ入力を受け取っていくときに,偶数ならそのまま出力することでACをとることができます。重複を考える必要も無いようです。
B - ASCII Art
問題文はこちらです。

この問題は,二次元配列やそれに準するデータ構造を使えるかを問うもののように見えます。計算量などは気にする必要がなさそうなので,入力を受け取り問題文の操作を適切に行うことでACをとれます。
C言語なら二次元配列を利用するのが一番自然です。char A[H][W]のような配列を宣言して,二重ループで入力の受け取りと出力をします。
A~i,j~番目の大文字アルファベットはASCIIコードの性質を利用することで簡単に出力することができます。ASCIIコードにおいて,大文字アルファベットはAから昇順に数値が割り当てられてあります。したがって,printf("%c", A[i][j] + 'A' - 1);のような形で実現することができます。(よくわからないという人は,C言語のprintfとASCIIコードについて調べてみるとよいと思います)
W個出力するたびに改行するのを忘れないようにしましょう。
また,二次元配列を使用するのが自然といいましたが,実は使用しなくても解くことができます。各入力をどのように置き換えるかはそれぞれの入力のみで決まり,ほかの入力のことを考慮する必要がありません。つまり,受け取った数が0なら即座に.を,それ以外なら'A' - 1を足したものを文字として出力すればよいです。
C - Merge Sequences
問題文はこちらです。

少し問題文を要約します。「二つの数列が与えられる。これらの要素をひとまとめにして,昇順に並べ替えた数列を作る。元の数列のi番目の要素は,新しく作った数列の何番目にあるでしょう?」という感じです。
制約から,要素のダブりはないです。したがって,求めたいもの(何番目か)はただ一つに定まります。シンプルに行くなら新しく作った数列を最初から順番に見ていき,等しくなった時にインデックスを出力すればACをとれるはずです。
ただしこのやり方では時間が間に合いません。最悪ケースを考えてみると分かりやすいです。元の二つの数列をA, Bとするとき,もしBの要素がAのどの要素より大きいとすると,結合して並べ替えた数列においてBの要素を探すときに必ずAの要素数分の無駄な探索が行われます。制約から,元の数列の要素数は10^5^個まであり得るので,このようなケースではBの要素を探そうとすると10^10^程度の操作が必要になります。どう考えても間に合いません。
ここで,新しい数列が整列済みだという事実を利用します。このようなときには 二分探索 をすることができ,一つの値を高速に探すことができます。知らなかった人は覚えておくとこの先役に立つと思います。
二分探索は要素数nに対して,およそlog(n)程度の計算量で値の探索をすることができます。また,全体をソートするためにおよそnlog(n)程度の計算量がかかります。以上より,nlog(n)程度の計算量で解くことができます。これは今回の制約下の最悪ケースで10^6^超えるかな~っていう程度です。
ACコード (前半は私のお手製ソート関数群です)
また,元の数列が整列済みだということを利用して,マージソートをするような感じでn + m程度の計算量でACをとることができるようです。(あえてACサンプルは載せません)
D - Bank
問題文はこちらです。

よくあるクエリを処理するやつです。今回は銀行の待合のアレみたいな問題です。
各クエリの処理方法を考えましょう。クエリ1はまだ呼ばれていない人のみが対象なので,単純にクエリ1が来た回数が分かればO(1)で答えることができます。クエリ2は実際に人が受付に向かう操作です。これ以外のクエリで受け受けに向かうことはないです。クエリ3は呼ばれている人のうち番号が一番若い人を再度呼び出すクエリです。
明らかにクエリ2,
3の処理が面倒くさそうです。簡単な解法を考えると,クエリ1で呼ばれた番号を集めておき,クエリ2で呼ばれたら削除,クエリ3が来たらその集合の最小値を出力すればよいです。これをシンプルに実装するなら順序付きの集合のようなデータ型を用いるのが良いです。(解説ではstd::setを勧めていました)なぜなら,指定した番号のデータに対して削除と最小番号の出力を同時にこなす必要があるからです。(キューや連想配列などだとどちらかの要件が面倒くさいです。)
私は少し違う方法をとりました。まず,制約からNの上限がそこまで大きくないので,全部配列に載せることができます。したがって,順序付き集合の代わりに配列を使用することができます。具体的にはこうです。要素数Nの配列を用意しておく。クエリ1は呼ばれた回数を出力,クエリ2が呼ばれたら配列のx番目に-1などを代入しておく。クエリ3が呼ばれたら-1の入っていない最小インデックスを出力する。この時,-1の入っていない最小インデックスの位置を常に保持しておくことで,クエリ3をO(N)で求めることができます。(O(N)と言っていますが,一回通過した場所には戻らないのでクエリ3のすべてを処理したとしてもN回以下の操作で答えることができます。)実はこの方法は上の解法と同等以上に高速です。
E - 2xN Grid
問題文はこちらです。

連続文字列が(数字)(長さ)という風に圧縮されている,元の長さLの文字列2つに対し,同じ位置で同じ数字が存在する場所の数の総和を求める問題です。
ランレングス 圧縮...ってコト!?
シンプルな問題ですが,この文字列をそのまま復元しようとすると,元の文字列長が長すぎてTLEします。(というか普通にメモリも使いすぎると思います。)したがって,何らかの方法で圧縮を戻さずに解を得る必要があります。
正直私にとって少しレベルの高い問題だったので,すっきりした解法ではないかもしれませんが,一応紹介します。
私はいたちごっこをしながらシュミレートする方法で解くことができました。まずは,各数字と圧縮長さをそれぞれv1[n1], len1[n1]とv2[n2], len2[n2]に格納します。
そしてn1のインデックスをi,n2のインデックスをjとします。基準点baseを最初0にしておきます。そして以下のアルゴリズムで解きます。
-
現在の総和
sum1, sum2を用意し,最初にlen1[0], len2[0]を入れておきます。答えをans=0とします。 -
v1[i]==v2[j]ならば「sum1とsum2のうち小さいほう - base」をansに足す。 -
sum1 == L && sum2 == Lならばansを出力し,終了 -
baseを
sum1とsum2のうち小さいほうで更新し,より小さいほうにlen〇[△ + 1]を足し,△ += 1としてインデックスを更新する。 -
2に戻る。
下にこのアルゴリズムの簡単な図解を載せておきます。元画像は AtCoderのコンテストページ からお借りしました。
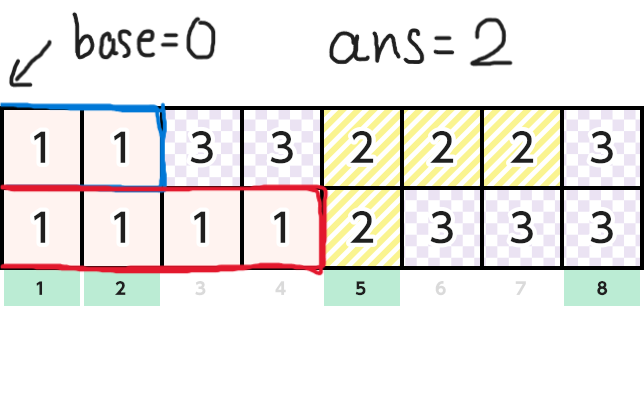
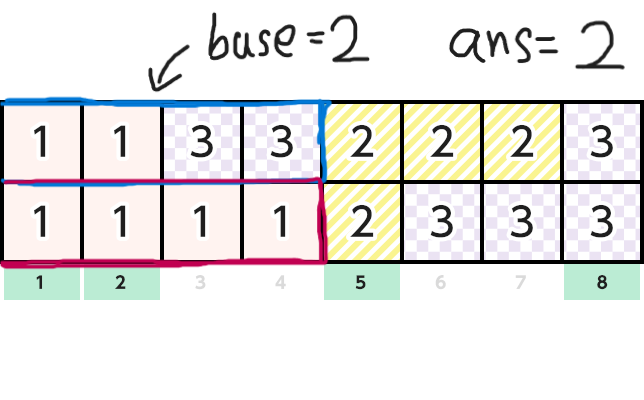
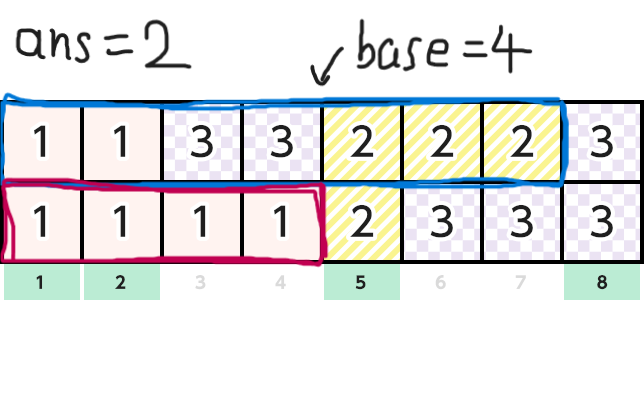
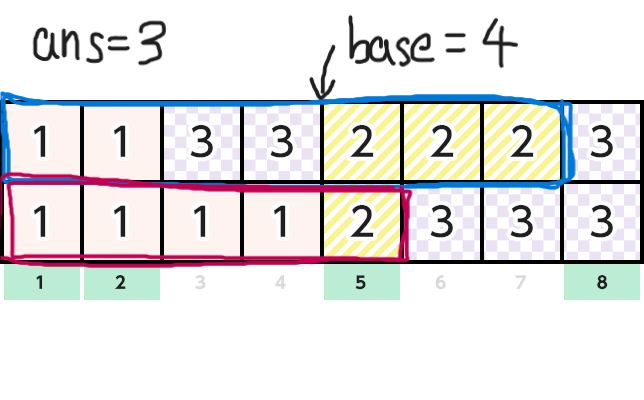
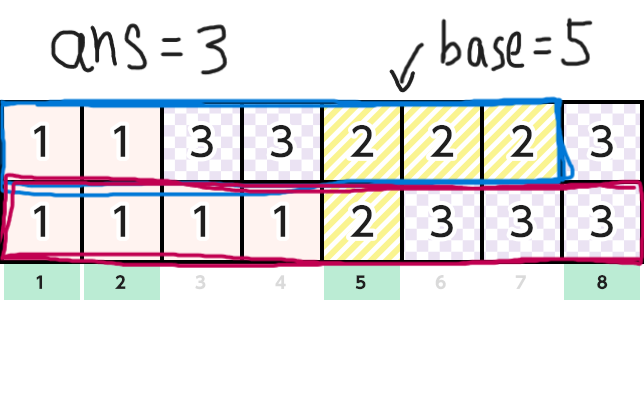
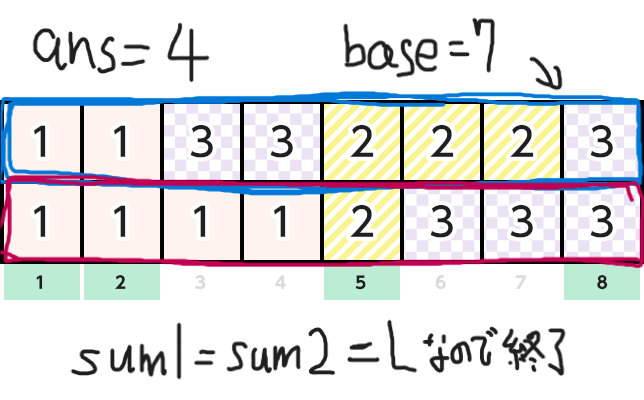
正直難しかった(小並感)
完走した感想
今回は4完でしたが,少しだけレートマイナスになってしまい残念です。今自分が使えるデータ構造が配列しかないので,今回のような問題に対応するためにもいくつかライブラリを整備しておこうかなと思いました。
あと地味に私は二分探索を書くのが下手だということが分かったので,実装について少し研究したいなと思っています。
コンテスト関係ないですが,今回のエントリ書くの結構時間かかりました。疲れた。
それではまた次回のエントリで