ABC288D - Range Add Query
Published on 2024-09-10Last Modified 2024-09-10
Table Of Contents
想定解法と全然異なる怪しい解法で通したので書きます。
問題概要
問題文
数列$X = (X _ 1, X _ 2, \dots, X _ n)$が良い数列であるとは、次の操作を0回以上行ってすべての要素を$0$に出来る事をいう。
- 長さ$K$の範囲と整数$c$を自由に選んで、選んだ区間にあるすべての数に$c$を加算する。
長さ$N$の数列$A$が与えられる。次の$Q$個のクエリに答えよ。
- $A$の$l _ i$番目から$r _ i$番目までを抜き出した長さ$r _ i - l _ i + 1$の数列が良い数列であるか判定する。
制約
- $1 \leq N \leq 2 \times 10 ^ 5$
- $1 \leq K \leq \min(10, N)$
- $-10 ^ 9 \leq A _ i \leq 10 ^ 9$
- $1 \leq Q \leq 2 \times 10 ^ 5$
- $K \leq r _ i - l _ i + 1$
解法
まずクエリ$O(N)$の解法を説明する。 与えられた数列$X$に対して、次の貪欲法を行う。
- 数列の左端から見ていく。今見ている場所が$X _ i$であるとする。そこを左端として区間加算が行えるならば、$c = -X _ i$として区間加算を行う。
この貪欲法を行った後、すべての要素が$0$であればYesである。
区間加算はimos法等で適切に処理することで$O(N)$で出来るため、クエリ$O(N)$の解法を得た。(正当性: 区間加算はどの順序で行っても結果は変わらない。よって、始点が早いものから行うとしてよい。今見ている場所を$0$以外にするような区間加算をしてしまうと、それ以降の区間加算で戻されることはないので、必ず$0$にするような区間加算をするしかない。)
この解法をベースに解く。 上記解法では数列$X$の値が非零である場所が$O(N)$個であるせいでクエリ$O(N)$から落とすことが出来ないでいる。もし仮に非零である要素が十分に少なければ、考慮すべき区間加算の数も少なくすることが出来る。
非零要素を絞るための準備として、「元の数列$A$を作るときに必要な長さ$K$の区間加算クエリがどうなるか」を考える。 これを求めるのは簡単で、上記で説明した貪欲法
- 数列の左端から見ていく。今見ている場所が$X _ i$であるとする。そこを左端として区間加算が行えるならば、$c = -X _ i$として区間加算を行う。
を数列$A$に対して適用してやればよい。(より詳しい方法は実装例を参照せよ。) 例えば、入力例1に対して以下の図のようになる。
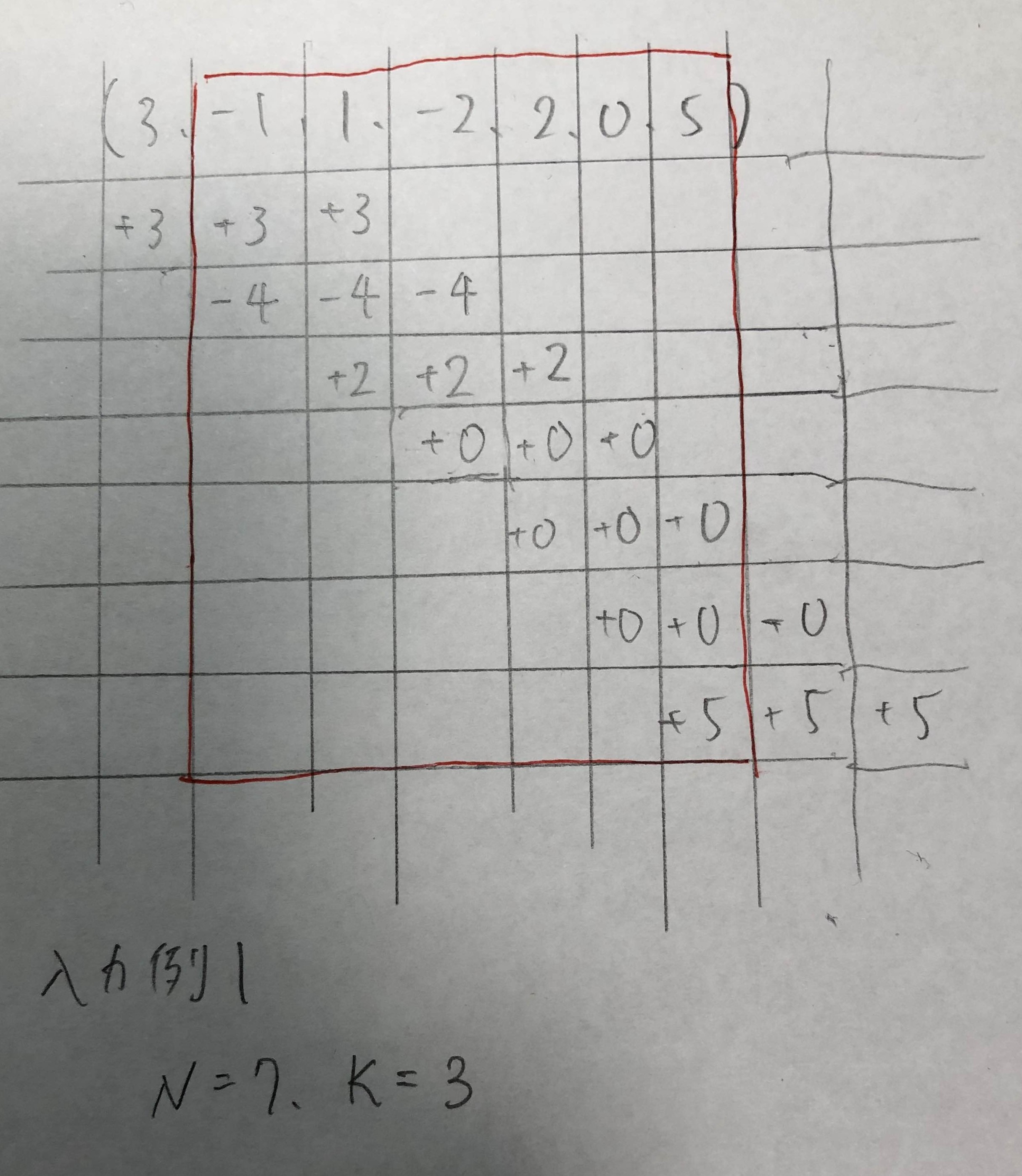
図の赤枠はクエリ2で与えられる区間である。
ここで次の事実に注目する。
- $[l _ i, r _ i - K - 1]$から始まる区間加算は、必ずキャンセルすることが出来る。
この性質により、クエリ2では-4, -4, -4と+2, +2, +2をそもそも考慮しなくてよいことがわかる。 結果的に、$(3, 3, 0, 0, 0, 5)$が良い数列であるかを判定する問題と等価になる。
整理すると、この状況下で考慮すべき区間加算クエリは、
- $l _ i$よりすこし前から始まっていて、区間内に影響するもの。
- $r _ i$よりすこし前から始まっていて、区間内で完結しないもの。
だけであることがわかる。これで非零要素を$O(K)$個に絞ることが出来た。 ここからナイーブに操作すると結局$O(N)$時間かかってしまうが、片方の区間加算の影響をもう片方に持っていき、長さ$O(K)$の区間が良い数列であるかを判定するようにすれば良い。 文章のみで説明するのが厳しいので、再び図を用いる。
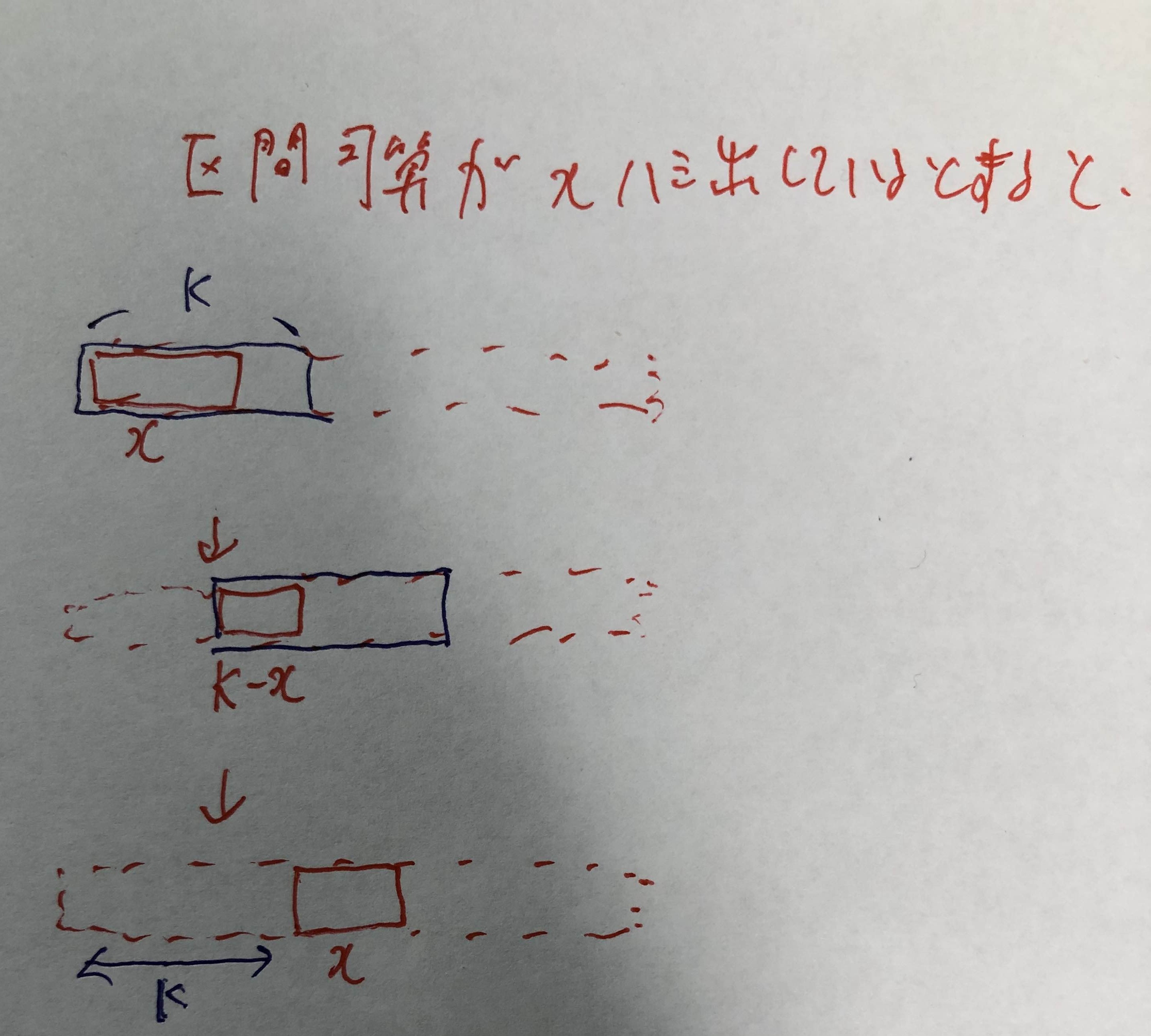
上記図のように、区間加算クエリ2回で幅$K$だけ影響をずらすことが出来る。最終的な移動位置は$O(1)$で求まるため、これで長さが高々$O(K)$である数列が良い数列であるか判定する問題に帰着できた。
判定はさぼると$O(K ^ 2)$で、いろいろと細かい部分を頑張ると$O(K)$になる。よって全体$O(N + QK)$で解ける。
実装例
$O(N + QK ^ 2)$である。面倒なのであまり説明はしないが、不明点があればTwitter等で聞いてほしい。
import std;
void main () {
int N, K; readln.read(N, K);
auto A = readln.split.to!(int[]);
// クエリO(N)かけられないよな~からスタート。
// Kが小さいなぁ~
// じゃあ逆に、最初の列を幅KのRAQで構築したと考えたらどうだろう。
// -> 重要なのは高々O(K)個のRAQだけで、クエリ区間に含まれるRAQはすべて打ち消すことが出来るじゃないか。
// -> じゃあ、片方に寄せ集めてこれを消せればOKではないですかね?
auto acc = new long[](N);
auto raq = new long[](N);
foreach (i; 0..N) {
// もらう
if (0 < i) acc[i] += acc[i - 1];
// そこから積む値は?
raq[i] = A[i] - acc[i];
// 実際積んでおく
acc[i] += raq[i];
if (i + K < N) acc[i + K] -= raq[i];
}
auto buf = new long[](N);
auto q = new int[](0);
void add (int i, long v) {
q ~= i;
buf[i] += v;
}
long get (int i) {
return buf[i];
}
void reset () {
foreach (v; q) buf[v] = 0;
q.length = 0;
}
int Q = readln.chomp.to!int;
auto ans = new string[](Q);
foreach (z; 0..Q) {
int l, r; readln.read(l, r);
l--, r--;
reset();
// 後ろ側のクエリ
foreach (i; 0..K - 1) {
add(r - i, raq[r - i]);
}
// 前側のクエリ
foreach (i; 0..K - 1) {
if (l - i - 1 < 0) break;
int rem = K - i - 1;
int d = (r - l + 1) / K;
add(l + d * K - 1 - (K - rem - 1), -raq[l - i - 1]);
if (l + d * K <= r) add(l + d * K, raq[l - i - 1]);
}
// 累積
{
int cur = r - 2 * K;
while (cur <= r) {
if (l < cur) add(cur, get(cur - 1));
cur++;
}
}
// 消せるかトライする。
{
int cur = r - 2 * K;
while (cur <= r) {
if (l <= cur && cur + K - 1 <= r) {
foreach (i; 0..K) {
add(cur + K - i - 1, -get(cur));
}
}
cur++;
}
}
bool ok = true;
foreach (i; 0..2 * K) {
if (r - i < l) break;
if (get(r - i) != 0) ok = false;
}
if (ok) {
ans[z] = "Yes";
}
else {
ans[z] = "No";
}
}
foreach (i; 0..Q) {
writeln(ans[i]);
}
}
void read (T...) (string S, ref T args) {
import std.conv : to;
import std.array : split;
auto buf = S.split;
foreach (i, ref arg; args) {
arg = buf[i].to!(typeof(arg));
}
}
終わりに
今日2時間くらい眺めてたら天啓が降ってきたので解いた。 天才以外お断りパズルみたいなやつから得られる知見が無さ過ぎて苦しい。 こういうのから共通点や思考のテクを抽出できる人が強いんだろうなって気持ちになって、すごく不快だった。
それはそれとして、配列の使用した場所だけを戻すことで計算量を下げるテクいいですよね。