ABC284参加記録
Published on 2023-01-07Last Modified 2023-09-22
Table Of Contents
今週もABCのお時間になりました。
みなさん,あけましておめでとうございます。本日2023年1月7日は記念すべき新年最初の AtCoder Beginners Contest でした。今週も参加してきたのでいつも通り参加記録です。
早速余談ですが,皆様は正月休みを有意義に使えましたか?私は久しぶりに帰省して,運動不足解消にと 鍋蓋山 に登りました。


冬ということもあって,道中も結構寒い時がありました。普通に服着ててこれなので,中学高校の持久走で言われた「走ってたら寒くないから」とか言うクッソ無責任な言葉を思い出したりしてました。

また,我らが UEC は1月5日から授業なので,年明けてすぐ帰りました。なお新年初授業は来てる人少なかった模様
閑話休題。それでは本編行きましょう
今回の結果
今回の提出はこんな感じでした。
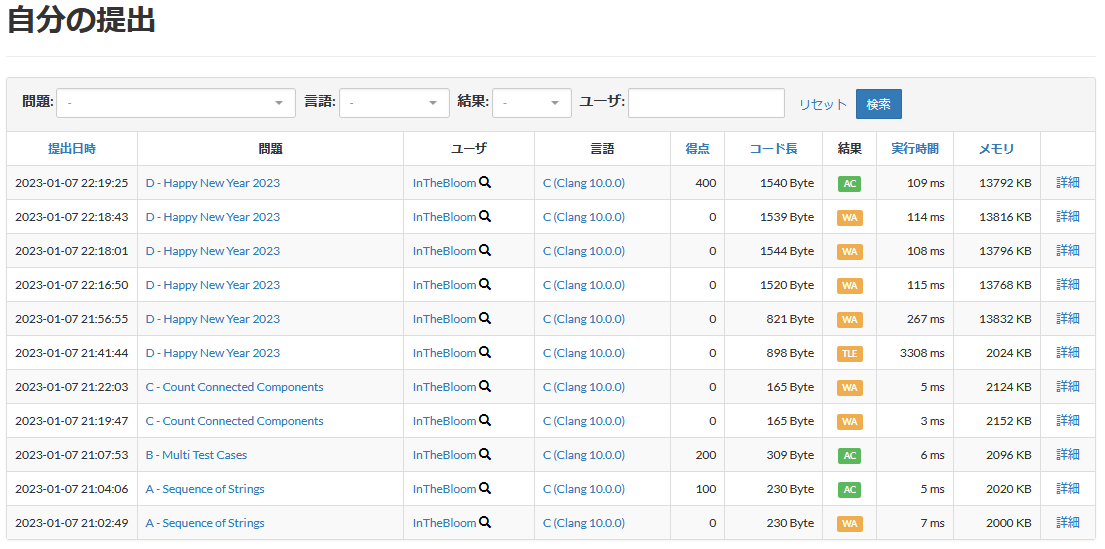
今回はA, B,
Dの三完でした。めちゃくちゃWAが多いのは気にしないでください。傷つきます。
なお,今回は初めてコンテスト中にD問題を解くことができました! うれしい!でもお前C解けないじゃん
今回のコンテストによるレーティング変動は以下の通りでした。
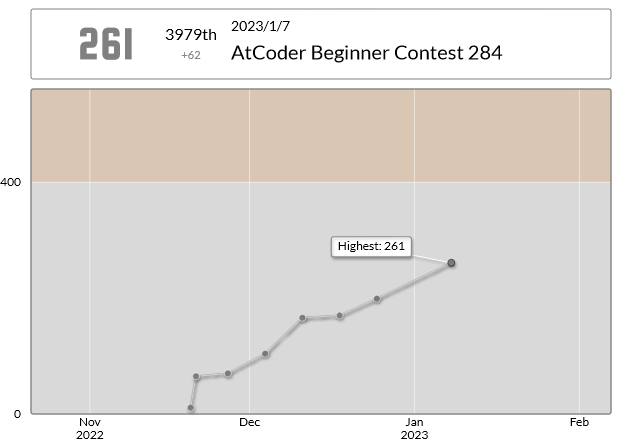
遂に茶色までの折り返しを超えることができました! やはりD問題が解けたのが大きかったようです。Cが解けなかったのに今までで最高のパフォーマンス(732でした。)を出すことができました。
各問題に対する解法など
いつも通りに私の考えたことなどを書いていきます。
A - Sequence of Strings
問題文は以下の通りでした。

文字列をN個受け取って,逆順で出力する問題でした。
一旦文字列をすべて保持して,あとから出力していけばオーケーです。ほかの言語についてはよくわかりませんが,C言語ならとりあえずいっつも理解が浅いせいで事故るからできるだけ避けたいけど二次元配列を使うと比較的アッサリ解けます。
具体的に言うと,char s[n][11]みたいなものを宣言して,scanf関数で&s[i][0]から受け取ればいいです。以下はAC通ったコードです。
#include <stdio.h>
int main(void) {
int n;
scanf("%i", &n);
char s[n][11];
for(int i = 0; n > i; i++) {
scanf("%s", &s[i][0]);
}
for(int i = n - 1; i >= 0; i--) {
printf("%s\n", s[i]);
}
return 0;
}
ちなみに,この問題の制約下では各文字列は10文字以下です。したがって,配列は終端文字'\0'を含めて11以上で宣言しなければいけません。私は普通に忘れててWA食らいました。
B - Multi Test Cases
問題文は以下の通りでした。

複数のテストケースに対して判定していくというちょっと変わった問題ですね。私がAtCoderに参加し始めてから初めて見るタイプでした。
幸い判定することは偶奇判定なので,2で割った余りを見ていけばOKです。ポイントを挙げるとするなら,答えはテストケースの順番に出力する必要があるので,入力を受け取るごとに出力をしていく感じで実装するとスマートです。以下ACコードです。
#include <stdio.h>
int main(void) {
int t;
scanf("%i", &t);
for(int i = 0; t > i; i++) {
int n;
int ans = 0;
scanf("%i", &n);
for(int i = 0; n > i; i++) {
int temp;
scanf("%i", &temp);
if(temp % 2 == 1) {
ans++;
}
}
printf("%i\n", ans);
}
return 0;
}
完全に余談ですが,最近変数のスコープの管理が少しだけうまくなったような気がします。
D - Happy New Year 2023
問題文は以下の通りでした。

一言でいうなら素因数分解をする問題です。ただし,今回の問題では対象となる数が2つの素数p, qによってp2qと表せることが分かっています。あと,この問題でもB問題と同じく複数のケースの判定を行う問題でした。
この問題を最も単純なアイデアから膨らませて考えていきます。
最も簡単な解き方は,単純にすべて試し割りしてみることです。「ある自然数は,それ以下の素数の積としてただ1通りに表すことができる」という事実を利用しています。要は素因数分解の一意性ってことです。換言すると,「ある数Nは,2からNまでのいずれかの素数で割っていくといずれ1になる」ということです。
例を挙げましょう。例えば2023は17×17×7,63は3×3×7に分解することができます。このことを利用すると以下のような実装が可能です。
for(int i = 2; n >= i; i++) {
if(n % i == 0) { // nを割ることができる数を発見
while(n % i == 0) { // 同じ数が複数回掛け算されている可能性もある
n /= i;
}
}
}
これをいい感じに今回の問題に当てはめると「原理的には」解くことができます。しかし,*実際には解くことができません。*競技プログラミングをやる方ならお分かりかと思いますが,今回の制約におけるNが9 × 1018以下という部分が引っ掛かります。つまり,無駄な計算が多すぎて実行時間に間に合いません。さて,どのような工夫が可能でしょうか?
私がこの問題を解くにあたって,まず足掛かりにしたのは「ある数Nは,Nの平方根より大きな素因数を多くても一つしか持たない」という事実です。残念ながらこの知識は当意即妙的に知らなかった状態からパッと思いつくのは難しいかなと(私は)思います。しかし,素数を扱うときに強力な武器になりえるので知らなかった人は憶えておくとよいかもしれません。よく考えると当たり前のことで,もしNの平方根より大きな素因数を2つもっていたとすると,その2数の積がすでにNを越えてしまうので,明らかに矛盾するからです。
この事実を使うと何が良いのでしょうか?それは,探索範囲が小さくできるからです。前述の事実から次のことが言えます。
-
NがNの平方根以下の素因数しか持たないとき,もちろんNの平方根までの探索で,すべての素因数を見つけることができる。
-
NがNの平方根より大きな素因数を持つ時,Nの平方根までの探索で見つけた素数でNを割ることで,残りの素因数を見つけることができる。
以上より,さっきまではNまで探索していたのに対して,Nの平方根までの探索でよいことを示すことができました。より具体的な方法を挙げると,Nの平方根まで「Nを割ることができる数」を見つけたらその都度見つけた数で限界まで割っていきます。探索がNの平方根まで終わったら,これまで割られてきたNを確認します。もしこの数が1になっていなければ,それは素数ということが確定しています。
この方法で問題を解くことができるでしょうか?残念ながら,おそらくまだ間に合いません。それはNの平方根が最大で109のオーダーに達するからです。
このアイデアは無駄だったのでしょうか?いや,まだあきらめるのは早いです。制約を見直してみましょう。今回はNは(重複を許して)3つの素因数を持ちます。先ほどの考え方を応用すると,Nの三乗根までの探索で少なくとも一つの素因数を見つけることが可能ということがいえます。これは,もしそれ以上の素因数を3つ以上持っていると先ほど示したものと同様の矛盾が生じるからです。
この時,探索範囲は最大で106のオーダーまで減少します。AtCoderでは, およそループを108くらいまで回せる そうなので,よほど定数倍を悪化させるような処理を書かなければおそらく通るでしょう。
基本的にはこのアイデアで通ると思います。が,私の実装ではまだ注意点があります。それは,三乗根までの探索ですべての素因数が確定するパターンと確定しないパターンに分かれるからです。
問題で言うところの素因数p(つまり,Nに二つ含まれているもの)を見つけることができれば,残りの素因数はNをpで割ることで見つけることができますが,もしqしか見つけられなかった場合,Nをqで割ることにより得られる数はp2となり,これをpに「ほぐす」作業が必要となります。私はこの処理を 二分探索 にて実装しました。
以下私のACコードです。
#include <stdio.h>
int disassembly(long long int *a, long long int *b, long long int *n, int *map) { // 素因数がすべてまたは2乗じゃないほうだけ見つかる
int flag;
for(int i = 2; 3000000 > i; i++) {
if(map[i] != 0) {
if(*n % map[i] == 0) {
*n /= map[i];
if(*n % map[i] == 0) { // このケースは確定
*a = map[i];
*n /= map[i];
*b = *n;
flag = 1;
break;
} else { // このケースはまだわからない
*b = map[i];
flag = 0;
break;
}
}
}
}
if(flag == 1) {
return 0;
} else {
return -1;
}
}
void Sqrt(long long int *a, long long int *n) {
long long int left, center, right;
left = 0;
if(*n > 3000000000) {
right = 3000000000;
} else {
right = *n;
}
for(; right - left > 10;) {
center = (right + left) / 2;
if(center * center > *n) {
right = center;
} else {
left = center;
}
}
for(; *n != left * left; left++) {}
*a = left;
}
int main(void) {
int t;
scanf("%i", &t);
int map[3000000]; // エラトステネス
for(int i = 0; 3000000 > i; i++) {
map[i] = i;
}
for(int i = 2; 1734 > i; i++) {
for(int j = 2 * i; 3000000 > j; j += j) {
map[j] = 0;
}
}
for(int i = 0; t > i; i++) {
long long int n;
scanf("%lli", &n);
long long int a, b; // 素因数
if(disassembly(&a, &b, &n, map) == 0) {
printf("%lli %lli\n", a, b);
} else {
Sqrt(&a, &n);
printf("%lli %lli\n", a, b);
}
}
return 0;
}
クソ長コードですまんかった。ポイントとしては,まず素数のリストを事前に エラトステネスの篩 を用いて事前計算しておくことで多少の軽量化を図っています。あとは二分探索でオーバーフローしないようにしています。いずれも制約ありきなので一般的に使えるコードではないです。
余談ですが,最近こんな風にvoidを返す関数にポインターの引数を与えることで,面倒くさい処理を外部委託するのにハマっています。それにしてもint *aみたいなやつを与えたときに*aって書くの面倒くさいですね。
C - Count Connected Components
問題文は以下の通りです。

無理でした。はい。
この問題に出てくる「グラフ」というのは,よくある「y = xのグラフ」のようなものではなくて,離散数学における「頂点と線をいくつか組み合わせた図形」のようなものらしいです。
例えば,以下のようなものがグラフです。(出典: AtCoder Beginners Contest284問題ページ より)
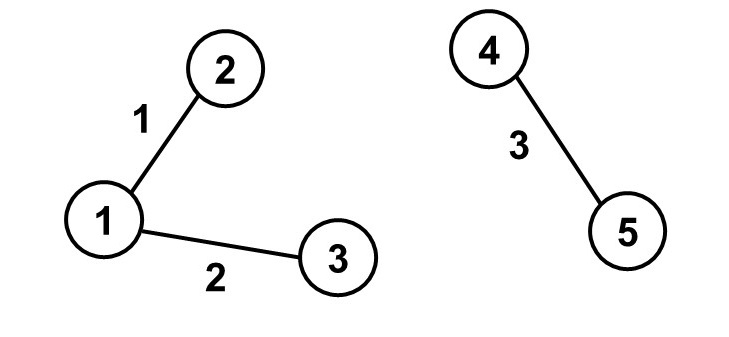
この問題の題意は多分「辺と頂点の情報が与えられるので,独立しているパーツの数を答えなさい」です。しかし,グラフの定義やそこから導かれる性質がよくわかっていなかったため,有効な解法がよくわかりませんでした。先にある程度グラフについて知らないと厳しそうです。

ということで,今後の課題ということにさせてください。
終わりに
今回の参加記録は以上です。ここまで読んでいただきありがとうございました。
余談ですが, AtCoder Problems にて今回のC問題のdifficultyを確認してきたのですが,なんと灰色の真ん中くらいでした。...うせやろ? どうやらグラフの探索は簡単めの典型のようです。次出たときには解けるようになりたいといいたいところですが,グラフを勉強するってどうすればいいんでしょうか...解説によると幅優先探索とかで解けるらしいです。 なんだよそれ
あと,最近はAtCoder Problems上の Boot camp for Beginners を少しずつ進めています。ついでにLongest Streak(ACを出した日の継続日)を伸ばそうと頑張っています。もしやっていない人がいたらおすすめです。
それでは次の記事でお会いしましょう。皆様にとって2023年がいい年になりますように!