ABC247F - Cards
Published on 2024-04-10Last Modified 2024-04-10
Table Of Contents
問題概要
問題文
$1$から$N$の番号がついた$N$枚のカードがあり、カード$i$の表には$P _ i$が、裏には$Q _ i$が書かれている。 ただし、$P = (P _ 1, \dots, P _ N)$及び$Q = (Q _ 1, \dots, Q _ N)$はそれぞれ$(1, \dots, N)$の置換である。
$N$枚のカードの部分集合であり、次の条件を満たすものがいくつあるかを$998244353$で割ったあまりを求めよ。
- $1$から$N$のどの数も、表または裏にその数が書かれたカードが、部分集合に少なくとも1枚含まれる。
制約
- $1 \leq N \leq 2 \times 10^5$
- $1 \leq P _ i, Q _ i \leq N$
解法
カードを3種類に分類する。
- 表と裏に書かれている数が同じ。
- 書かれた数の集合が一致するカードが他に存在する。
- その他。
まず、1のカードは条件を満たすために取るしかない。
2のカードは、少なくとも片方を取る必要があるため、このペア1組につき解が3倍になる。 もう少し詳細に説明しよう、カードに書かれた数の集合が$\lbrace x, y \rbrace$であるものが2枚存在するとする。 このとき、部分集合に$x$または$y$が含まれるようにするためには、この2枚のうち少なくとも1枚は取らなければいけない。 よって、これらカードについて(とる/とらない)、(とらない/とる)、(とる/とる)の3通りの選択肢が存在し、これは他のカードの選択に影響を及ぼさないため、独立である。 すなわち、ペアが1組増えるごとに部分集合の数は3倍になる。
3のカードについて考える。これらどう取ればよいかが一番難しい部分であり、この問題の本質である。
まずはカードを頂点とみなして、同じ数を含むカードに無向辺をはることにする。 このとき、カードに書かれている任意の数は、全体で必ず2個存在する。これはカード1とカード2の定義を考えれば明らかである。 すなわち、任意の頂点に必ず2辺が接続することになる。
このようにしてできたグラフは、各連結成分は必ず全体がただ一つの閉路に含まれる。すわなち、円環になる。 これは次の命題が真であることから言える。
「連結で単純な$N$頂点$N$辺の無向グラフで、すべての頂点の出次数が2であるとき、このグラフはちょうど一つの閉路を持ち、すべての頂点は閉路に含まれる。」
証明
(i) ちょうど一つの閉路を持つことまず、次の命題を帰納法により示す。
「連結グラフは、全域木を部分グラフに含む」
証明
グラフ$G$の辺集合$E$とする。 $\vert E \vert = 0$のときは、グラフが連結であるという仮定から、$G$は孤立頂点である。このとき命題は成立。$\vert E \vert = k$のときに成立すると仮定する。 $\vert E \vert = k + 1$のとき、 $G$が閉路を含まないならば、$G$は木の定義を満たすので、$G$そのものが全域木である。 $G$が閉路を含むならば、閉路の任意の辺を切断すると、$\vert E \vert = k$に帰着する。
したがって、グラフが連結であれば全域木が存在する。
折りたたみ内折りたたみ終わり。
この命題により、今考えているグラフは全域木を含むことが分かる。任意の全域木を選び、木に含まれない辺を$e = (u, v)$とする。 このとき木の性質として、$u, v$パスは一意に定まる。 すなわち、元の(この全域木に$e$を追加したグラフ)は、$u, v$パス → $e$というただ一つの閉路を持つ。
(ii) すべての頂点が閉路に含まれること
任意の頂点を選び、$v _ 0$とする。$v _ 0$に隣接する頂点を一つ選び、$v _ 1$とする。 $v _ 1$の$v _ 0$でない方の隣接頂点を$v _ 2$とする。 これを繰り返していく。
すると、グラフは閉路を持つため、いつか$v _ k$は訪問済みの頂点になる。 このとき、$v _ 0$以外の頂点($v _ x$とする)にたどり着いたとすると、$v _ x$は出次数2の仮定を満たさない。 さらに、$v _ 0$にたどりついたときに全頂点を訪問済みになっていない場合、連結であるという仮定を満たさない。
よって、頂点$v _ 0$からはじまり、すべての頂点をちょうど1回訪問し、頂点$v _ 0$に戻ってくるというパターン以外はありえない。 これはすべての頂点が閉路に含まれるということである。
折りたたみ終わり。
つまり、グラフは次の図のようになる。
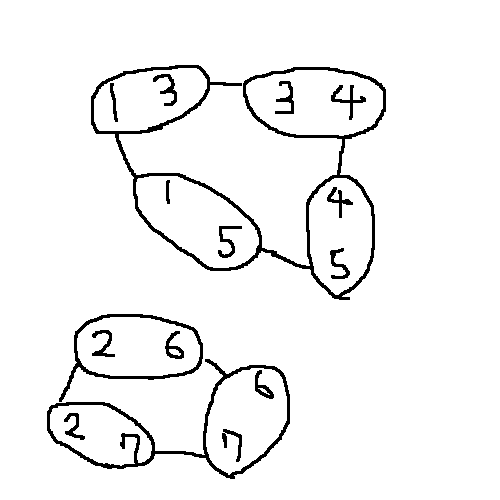
ある一つの連結成分に対して考えると、条件を満たすようなカードの選び方は、「取らないカードの隣接頂点は必ず取る」であることが分かる。 必要性は、取らないカードが2連続するとき、そのカードをつなぐ数を取れなくなることによる。 十分性も同様に、任意の数は隣り合うカードのどちらかを取れば含めることができることにより説明できる。
上の図上部の連結成分に対しては、$\lbrace \lbrace 1, 3 \rbrace, \lbrace 1, 5 \rbrace \rbrace$は条件を満たすが、 $\lbrace \lbrace 1, 3 \rbrace, \lbrace 3, 4 \rbrace \rbrace$は条件を満たさない。
あとはこの数え上げを解ければよい。 これを解くために、次の問題を考えよう。
列$A = (A _ 0, A _ 2, \dots, A _ {k - 1}), A _ i \in \lbrace 0, 1 \rbrace$であって、次の条件を満たすものはいくつか?
- $0 \leq A _ i + A _ {i + 1 \mod k}$
この有効な列$A$はそのまま有効なカードのとり方と対応している。 具体的には、閉路の任意の頂点を固定し、そこから時計回りに頂点を並べた列$(v _ 0, v _ 1, \dots, v _ k)$を考える。 このとき、$v _ i$を取るかどうかを$A _ i$の値によって決めることで対応付けることができる。
隣との和が$0$でなければ良いのだから、$0$を使用したいときは$0$と$1$を束ねて使用することにすると見通しが良くなる。 すなわち、$x$個の$10$と、$k - 2x$個の$1$を並べる問題だと考えれば良い。
ただし、この方法だと先頭が$0$であるような列が生成できない。 これは、先頭を$0$、末尾を$1$に固定した状態で、$x - 1$個の$10$と$k - 2x$個の$1$を並べる場合の数を足すことで回避できる。
この方法により、任意の有効な列をちょうど1回数えることができる。 これは、次の理由による。
- ある有効な列をこの方法により前から構成するとき、続く文字列が$11, 1$のときは$1$を配置するしかなく、$10$のときは$10$を配置するしか無いため、構成方法が一意に定まる。
- $10$と$1$をどのように並べても、$00$を作ることはできない。
これらは二項係数の計算ができれば解ける。 適切に前計算することで各ケース$O(1)$時間で解けるから、全体で$O(k)$時間である。
これで、有効な列$A$の数え上げが解けた。 もとの問題に戻ろう。
一つの連結成分の頂点のとり方は他の連結成分のとり方に影響しないため、場合の数はそれらすべての積になる。 また、各連結成分の次数の和は$O(N)$個であるため、全体$O(N)$時間で解ける。
実装例
import std;
void main () {
int N = readln.chomp.to!int;
auto P = readln.split.to!(int[]);
P[] -= 1;
auto Q = readln.split.to!(int[]);
Q[] -= 1;
solve(N, P, Q);
}
void solve (int N, int[] P, int[] Q) {
// カードを3種類に分類する。
// 1. 表と裏で同じ数が書いている
// 2. 同じ数字の割り当てのカードが存在する
// 3. 1, 2に当てはまらない
// 1は必ずとる必要があるので、これを除く。
// 2は少なくとも片方をとればよく、この枚数をxとして、任意の取り方が3^(x/2)倍になる。
// 3をどう取るか?が本質
const long MOD = 998244353;
int[Tuple!(int, int)] count;
foreach (i; 0..N) {
count[tuple(min(P[i], Q[i]), max(P[i], Q[i]))]++;
}
int type1 = 0;
foreach (i; 0..N) {
if (tuple(i, i) in count) {
type1++;
}
}
int type2 = 0;
foreach (key, val; count) {
if (val == 2) {
type2++;
}
}
int[] type3;
auto idx = new int[][](N, 0);
foreach (i; 0..N) {
idx[P[i]] ~= i;
idx[Q[i]] ~= i;
}
auto UF = UnionFind(N);
foreach (I; idx) {
if (0 < I.length) {
UF.unite(I[0], I[1]);
}
}
foreach (i; 0..N) {
if (UF.root(i) == i && 3 <= UF.GroupSize(i)) type3 ~= UF.GroupSize(i);
}
// 3のカードを(a, b)のように考えて、同じ数字を隣り合わせに配置してみると、円環になる。
// この時、空白が高々サイズ1であることが有効なとり方の必要十分条件。
// とるのととらないのをペア(ox)にしてやれば、何個とらないかで場合分けして組み合わせに帰着できる。
// 具体的な帰着について考える。
// oとoxの並べ替えと考えると、多項係数になる。
// 頭がxになるようなものだけ無理なので、そのようなケースのみxoを使う数え上げもする。
// WA -> 多分議論は合っていて、円環が複数できうるケースに対応できていないものと考えられる。
alias m = PrimeModuloFactorial!MOD;
m.build(N);
long ans = 1;
foreach (t3; type3) {
long prod = 0;
foreach (t; 0..N) {
if (t3 < 2 * t) break;
int r = t3 - 2 * t;
if (t == 0) {
prod++;
continue;
}
{ // ox数え上げ
long add = m.factorial(t + r);
add *= m.factorial_inv(t);
add %= MOD;
add *= m.factorial_inv(r);
add %= MOD;
prod += add;
prod %= MOD;
}
{ // xo数え上げ
long add = m.factorial(t + r - 1);
add *= m.factorial_inv(t - 1);
add %= MOD;
add *= m.factorial_inv(r);
add %= MOD;
prod += add;
prod %= MOD;
}
}
ans *= prod;
ans %= MOD;
}
ans *= mod_pow(3, type2, MOD);
ans %= MOD;
writeln(ans);
}
// check mod_inv
static assert(__traits(compiles, mod_inv(998244353, 1_000_000_007)));
template PrimeModuloFactorial (ulong M)
if ((1 <= M && M < int.max)
&& ((x) {
for (int i = 2; i < x; i++) {
if (x < 1L*i*i) break;
if (x % i == 0) return false;
}
return true;
})(cast(int) M))
{
import std.conv : to;
import std.format : format;
private:
long[] fact, fact_inv;
int N = 0;
long MOD = M;
public:
void build (ulong N_) {
N = N_.to!int;
fact.length = fact_inv.length = N+1;
fact[0] = 1;
for (int i = 1; i <= N; i++) fact[i] = i * fact[i-1] % MOD;
fact_inv[N] = mod_inv(fact[N], MOD);
for (int i = N; 0 < i; i--) fact_inv[i-1] = i * fact_inv[i] % MOD;
}
long binom (ulong n_, ulong k_)
in {
assert((n_ < k_
|| (n_ <= N && k_ <= N)),
format("Out of range of pre-calculation. MAX = %s, n = %s, k = %s.", N, n_, k_),
);
}
do {
int n = n_.to!int;
int k = k_.to!int;
if (n < k) return 0;
long res = fact[n] * fact_inv[k] % MOD;
return res * fact_inv[n-k] % MOD;
}
long factorial (ulong x_)
in {
assert(x_ <= N,
format("Out of range of pre-calculation. MAX = %s, x = %s.", N, x_),
);
}
do {
int x = x_.to!int;
return fact[x];
}
long factorial_inv (ulong x_)
in {
assert(x_ <= N,
format("Out of range of pre-calculation. MAX = %s, x = %s.", N, x_)
);
}
do {
int x = x_.to!int;
return fact_inv[x];
}
}
// check mod_pow
static assert(__traits(compiles, mod_pow(2, 10, 998244353)));
long mod_inv (const long x, const long MOD)
in {
import std.format : format;
assert(1 <= MOD, format("MOD must satisfy 1 <= MOD. Now MOD = %s.", MOD));
assert(MOD <= int.max, format("MOD must satisfy MOD*MOD <= long.max. Now MOD = %s.", MOD));
}
do {
return mod_pow(x, MOD-2, MOD);
}
long mod_pow (long a, long x, const long MOD)
in {
assert(0 <= x, "x must satisfy 0 <= x");
assert(1 <= MOD, "MOD must satisfy 1 <= MOD");
assert(MOD <= int.max, "MOD must satisfy MOD*MOD <= long.max");
}
do {
// normalize
a %= MOD; a += MOD; a %= MOD;
long res = 1L;
long base = a;
while (0 < x) {
if (0 < (x&1)) (res *= base) %= MOD;
(base *= base) %= MOD;
x >>= 1;
}
return res % MOD;
}
class UnionFind_Array {
/*
* VERYFYIED
* - uniteとsame : yosupo judge (https://judge.yosupo.jp/problem/unionfind)
*
* UNVERYFYIED
* - countGroups
* - GroupSize
* - enumGroups
*/
private:
int N;
int[] parent;
int[] size;
this (int N)
in {
assert(0 <= N, "N must be positive integer.");
}
do {
this.N = N;
parent = new int[](N);
size = new int[](N);
foreach (i; 0..N) {
parent[i] = i;
size[i] = 1;
}
}
int root (int x)
in {
assert(0 <= x && x < N);
}
do {
if (parent[x] == x) return x;
return parent[x] = root(parent[x]);
}
bool same (int x, int y)
in {
assert(0 <= x && x < N);
assert(0 <= y && y < N);
}
do {
return root(x) == root(y);
}
void unite (int x, int y)
in {
assert(0 <= x && x < N);
assert(0 <= y && y < N);
}
do {
int larger, smaller;
if (GroupSize(x) <= GroupSize(y)) {
larger = root(y);
smaller = root(x);
} else {
larger = root(x);
smaller = root(y);
}
if (larger == smaller) return;
parent[smaller] = larger;
size[larger] += size[smaller];
}
int countGroups () {
int res = 0;
foreach (i; 0..N) if (root(i) == i) res++;
return res;
}
int GroupSize (int x)
in {
assert(0 <= x && x < N);
}
do {
return size[root(x)];
}
int[][] enumGroups (int x)
in {
assert(0 <= x && x < N);
}
do {
int[][] mp = new int[][](N, 0);
foreach (i; 0..N) {
mp[root(i)] ~= i;
}
int[][] res;
foreach (m; mp) {
if (m.length == 0) continue;
res ~= m;
}
return res;
}
void reset (int N = this.N)
in {
assert(0 <= N, "N must be positive integer.");
}
do {
if (N != this.N) {
this.N = N;
parent.length = size.length = N;
}
foreach (i; 0..N) {
parent[i] = i;
size[i] = 1;
}
}
}
auto UnionFind (int N) {
return new UnionFind_Array(N);
}
UnionFindで各閉路の連結成分のサイズを取得する実装になっている。
UnionFindを用いた影響により、微妙に線形時間ではなくなっていることに注意してほしい。
solveより下のコードはすべてライブラリである。
終わりに
難しかったです。かなり時間がかかりました。 カードを分類することは本質的ではないものの、分類することによって、タイプ3のカードの集合が成すサイクルに着目する発想をすることができました。
サイクルから条件を満たすように取る方法の数え上げについては、公式解説により自然な言い換えとその解法が載っています。そちらはまだ理解していませんが、次解くときにはその方針が見えるようになっていれば良いなと思います。
グラフに関する用語の定義は 37zigen を参考にしました。 全域木に関する議論の主張及び証明は、 電気通信大学のpdf を参考にしました。 「連結で単純なN頂点N辺の無向グラフで、すべての頂点の出次数が2であるとき、このグラフはちょうど一つの閉路を持ち、すべての頂点は閉路に含まれる。」という命題に関する議論は、@marble_kyoproさん、@Seed57_cashさん、@coindarwさんに助言頂きました。
ありがとうございました。